题目内容
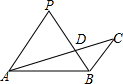 如图,若AP=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=5,PD=3,则AD•DC等于( )
如图,若AP=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=5,PD=3,则AD•DC等于( )| A、16 | B、15 | C、7 | D、6 |
考点:相似三角形的判定与性质
专题:
分析:如图,作辅助线;证明∠Q=∠C,结合∠QDA=∠BDC,得到△ADQ∽△BDC,列出比例式
=
,化为等积式即可解决问题.
| QD |
| DC |
| AD |
| BD |
解答: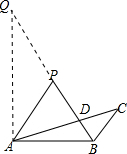 解:如图,延长BP到Q,使PQ=BP;连接AQ;
解:如图,延长BP到Q,使PQ=BP;连接AQ;
则∠Q=∠PAQ,∠APB=∠Q+∠PAQ=2∠Q;
∵∠APB=2∠ACB,
∴∠Q=∠C,而∠QDA=∠BDC,
∴△ADQ∽△BDC,
∴
=
,
即AD•DC=QD•BD,而DQ=5+3=8,BD=2,
∴AD•DC=16,
故选:A.
 解:如图,延长BP到Q,使PQ=BP;连接AQ;
解:如图,延长BP到Q,使PQ=BP;连接AQ;则∠Q=∠PAQ,∠APB=∠Q+∠PAQ=2∠Q;
∵∠APB=2∠ACB,
∴∠Q=∠C,而∠QDA=∠BDC,
∴△ADQ∽△BDC,
∴
| QD |
| DC |
| AD |
| BD |
即AD•DC=QD•BD,而DQ=5+3=8,BD=2,
∴AD•DC=16,
故选:A.
点评:此题主要考查了相似三角形的判定及其性质的应用问题;作辅助线,构造相似三角形,灵活运用有关定理来分析、判断、推理或解答是解题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
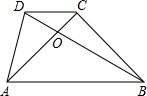 在四边形ABCD中,AB∥CD,对角线AC、BD交于点O,3CD=2AB,则S△ADC:S△AOB=( )
在四边形ABCD中,AB∥CD,对角线AC、BD交于点O,3CD=2AB,则S△ADC:S△AOB=( )| A、4:9 | B、6:9 |
| C、8:9 | D、10:9 |
 如图,AC∥BD∥EF,AC=20,BD=80,则EF=
如图,AC∥BD∥EF,AC=20,BD=80,则EF=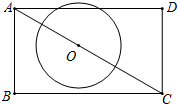 如图,已知矩形ABCD中,AB=2,BC=2
如图,已知矩形ABCD中,AB=2,BC=2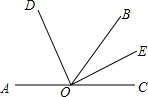 如图所示,∠AOB与∠BOC互为补角,OD平分∠AOB,OE平分∠BOC,求∠DOE的度数.
如图所示,∠AOB与∠BOC互为补角,OD平分∠AOB,OE平分∠BOC,求∠DOE的度数. 如图,拦水坝的横断面为梯形ABCD,根据图中的数据求:
如图,拦水坝的横断面为梯形ABCD,根据图中的数据求: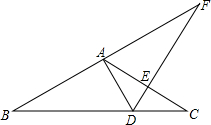 如图,等腰三角形ABC中,AB=AC,点D在BC边上,连接AD,点E在直线
如图,等腰三角形ABC中,AB=AC,点D在BC边上,连接AD,点E在直线 一自动喷灌设备的喷流情况如图所示,设水管OA在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线成45°角,水流最高点B比喷头A高2米.
一自动喷灌设备的喷流情况如图所示,设水管OA在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线成45°角,水流最高点B比喷头A高2米.