题目内容
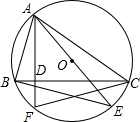 如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O的弦,且AF⊥BC于D点.求证:
如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O的弦,且AF⊥BC于D点.求证:(1)△ADC∽△ABE;
(2)BE=CF.
考点:相似三角形的判定与性质,圆周角定理
专题:证明题
分析:(1)利用圆周角定理以及相似三角形的判定得出即可;
(2)利用相似三角形的性质得出∠CAD=∠BAE,进而求出BE=CF.
(2)利用相似三角形的性质得出∠CAD=∠BAE,进而求出BE=CF.
解答:证明:(1)∵AF⊥BC,
∴∠ADC=90°,
∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠ADC=∠ABE,
又∵∠E=∠ACB,
∴△ADC∽△ABE;
(2)∵△ADC∽△ABE,
∴∠CAD=∠BAE,
∴
=
,
∴BE=FC.
∴∠ADC=90°,
∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠ADC=∠ABE,
又∵∠E=∠ACB,
∴△ADC∽△ABE;
(2)∵△ADC∽△ABE,
∴∠CAD=∠BAE,
∴
 |
| BE |
 |
| FC |
∴BE=FC.
点评:此题主要考查了相似三角形的判定与性质以及圆周角定理,正确把握相似三角形的判定定理是解题关键.

练习册系列答案
相关题目
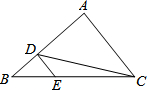 如图,在△ABC中,D,E分别是AB,BC上的点,且DE∥AC,若S△BDE:S△CDE=1:3,则S△BDE:S△ACD=( )
如图,在△ABC中,D,E分别是AB,BC上的点,且DE∥AC,若S△BDE:S△CDE=1:3,则S△BDE:S△ACD=( )| A、1:5 | B、1:9 |
| C、1:10 | D、1:12 |
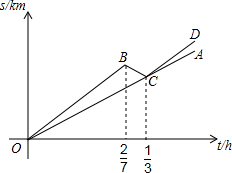 某自行车队根据队员速度的不同,分为快1组、快2组、慢1组和慢2组四个小组,在该车队的一次训练中,快1组和慢1组从甲地行进到乙地,剩下的组从乙地行进到甲地.快1组和慢1组同时从甲地出发,快1组的队员以高于慢1组队员10km/h的速度前行,快1组行驶一段时间后因某些原因又往回行驶(在往返过程中速度不变),最终与慢1组汇合,汇合后两组继续以各自的速度向乙地行进.设快1组和慢1组行驶的时间为t,与甲地的距离为s,s与t之间的函数图象如图所示.
某自行车队根据队员速度的不同,分为快1组、快2组、慢1组和慢2组四个小组,在该车队的一次训练中,快1组和慢1组从甲地行进到乙地,剩下的组从乙地行进到甲地.快1组和慢1组同时从甲地出发,快1组的队员以高于慢1组队员10km/h的速度前行,快1组行驶一段时间后因某些原因又往回行驶(在往返过程中速度不变),最终与慢1组汇合,汇合后两组继续以各自的速度向乙地行进.设快1组和慢1组行驶的时间为t,与甲地的距离为s,s与t之间的函数图象如图所示.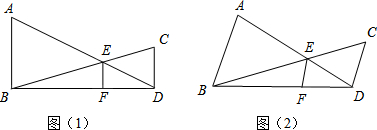
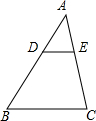 如图,DE∥BC,AD:DB=2:3,则△AED和△ABC的相似比为
如图,DE∥BC,AD:DB=2:3,则△AED和△ABC的相似比为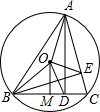 如图,锐角△ABC内接于圆O,AD⊥BC,BE⊥AC,OM⊥BC,垂足分别为D、E、M.
如图,锐角△ABC内接于圆O,AD⊥BC,BE⊥AC,OM⊥BC,垂足分别为D、E、M.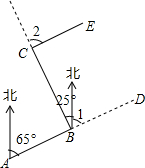 林湾乡修建一条灌溉水渠,如图,水渠从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村水渠从C村沿什么方向修建,可以保持与AB的方向一致?
林湾乡修建一条灌溉水渠,如图,水渠从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村水渠从C村沿什么方向修建,可以保持与AB的方向一致?