题目内容
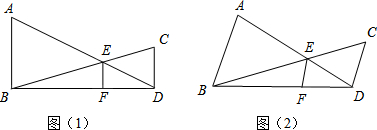
（1）如图（1），AB⊥BD，CD⊥BD，AD与BC相交于点E，EF⊥BD，试说明：
+
=
；
（2）如图（2）若AB∥EF∥CD，请直接回答（1）中结论是否成立；
（3）在（2）中找出S△ABD、S△BED和S△BDC之间的数量关系，并说明理由．
| 1 |
| AB |
| 1 |
| CD |
| 1 |
| EF |
（2）如图（2）若AB∥EF∥CD，请直接回答（1）中结论是否成立；
（3）在（2）中找出S△ABD、S△BED和S△BDC之间的数量关系，并说明理由．
考点：相似三角形的判定与性质
专题：
分析：（1）易证EF∥AB∥CD，则△ABD∽△EFD，根据相似三角形的对应边的比相等，即可证得
=
，同理
=
，两式相加即可证得；
（2）由题意知，两直线平行是很关键的条件，要根据三角形平行线分线段成比例，找出关系，然后相加就得到结果；
（3）要用到第一问的结论，作出各个三角形的高，再把各面积用边表示出来，即可找到关系．
| EF |
| AB |
| DF |
| BD |
| EF |
| CD |
| BF |
| BD |
（2）由题意知，两直线平行是很关键的条件，要根据三角形平行线分线段成比例，找出关系，然后相加就得到结果；
（3）要用到第一问的结论，作出各个三角形的高，再把各面积用边表示出来，即可找到关系．
解答：（1）证明：∵AB⊥BD，EF⊥BD，
∴EF∥AB，
∴△ABD∽△EFD，
∴
=
，
同理
=
，
∴
+
=
+
=
=1，即（
+
）•EF=1，
∴
+
=
；
（2）成立．
证明：∵AB∥EF，
∴
=
，
∵CD∥EF
∴
=
，
∴∴
+
=
+
=
=1，
∴
+
=
；
（3）关系式为：
+
=
．
证明如下：分别过A作AM⊥BD于M，过E作EN⊥BD于N，过C作CK⊥BD交BD的延长线于K
由题设可得：
+
=
，
∴
+
=
，即
+
=
，
又∵
•BD•AM=S△ABD，
•BD•CK=S△BCD，
∴
•BD•EN=S△BED，
∴
+
=
．
∴EF∥AB，
∴△ABD∽△EFD，
∴
| EF |
| AB |
| DF |
| BD |
同理
| EF |
| CD |
| BF |
| BD |
∴
| EF |
| AB |
| EF |
| CD |
| DF |
| BD |
| BF |
| BD |
| BD |
| BD |
| 1 |
| AB |
| 1 |
| CD |
∴
| 1 |
| AB |
| 1 |
| CD |
| 1 |
| EF |
（2）成立．
证明：∵AB∥EF，
∴
| EF |
| AB |
| DF |
| BD |
∵CD∥EF
∴
| EF |
| CD |
| BF |
| BD |
∴∴
| EF |
| AB |
| EF |
| CD |
| DF |
| BD |
| BF |
| BD |
| BD |
| BD |
∴| 1 |
| AB |
| 1 |
| CD |
| 1 |
| EF |
（3）关系式为：
| 1 |
| S△ABD |
| 1 |
| S△BDC |
| 1 |
| S△BED |
证明如下：分别过A作AM⊥BD于M，过E作EN⊥BD于N，过C作CK⊥BD交BD的延长线于K
由题设可得：
| 1 |
| AM |
| 1 |
| CK |
| 1 |
| EN |
∴
| 2 |
| BD•AM |
| 2 |
| BD•CK |
| 2 |
| BD•EN |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
又∵
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴
| 1 |
| S△ABD |
| 1 |
| S△BDC |
| 1 |
| S△BED |
点评：考查了相似三角形的判定与性质，正确通过相似三角形的性质把线段的比进行转化是关键．同时考查了平行线分线段成比例定理的运用．
练习册系列答案
阅读快车系列答案
相关题目
把27430用科学记数法表示应是（ ）
| A、0.2743×103 |
| B、27.43×103 |
| C、274.3×10 |
| D、2.743×104 |
如图，如果∠AON=∠BOM，OC平分∠MON，那么图中除∠AON=∠BOM外，相等的角还有（ ）| A、1对 | B、2对 | C、3对 | D、4对 |
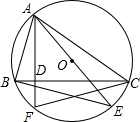如图，△ABC是⊙O的内接三角形，AE是⊙O的直径，AF是⊙O的弦，且AF⊥BC于D点．求证：
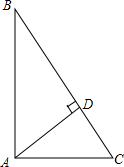如图，在△ABC中，∠BAC=90°，AD⊥BC，AB=4，DC=
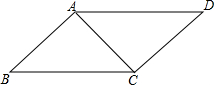如图，在四边形ABCD中，∠BAC=∠ACD=90°，∠B=∠D．若AB=3cm，