题目内容
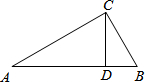如图，在Rt△ABC中，∠C=90°，CD⊥AB，D为垂足，且BC：AC=2：3，那么BD：AD的值为考点：相似三角形的判定与性质
专题：计算题
分析：先证明Rt△ACD∽Rt△ABC，利用相似比得到AD=
，同理可得Rt△BCD∽Rt△BAC，得到BD=
，则
=（
）2，然后把BC：AC=2：3代入计算．
| AC2 |
| AB |
| BC2 |
| AB |
| BD |
| AD |
| BC |
| AC |
解答：解：∵CD⊥AB，
∴∠ADC=90°，
而∠CAD=∠BAC，
∴Rt△ACD∽Rt△ABC，
∴AC：AB=AD：AC，
∴AD=
，
同理可得Rt△BCD∽Rt△BAC，
∴BC：AB=BD：BC，
∴BD=
，
∴
=
=（
）2=（
）2=
．
故答案为
．
∴∠ADC=90°，
而∠CAD=∠BAC，
∴Rt△ACD∽Rt△ABC，
∴AC：AB=AD：AC，
∴AD=
| AC2 |
| AB |
同理可得Rt△BCD∽Rt△BAC，
∴BC：AB=BD：BC，
∴BD=
| BC2 |
| AB |
∴
| BD |
| AD |
| ||
|
| BC |
| AC |
| 2 |
| 3 |
| 4 |
| 9 |
故答案为
| 4 |
| 9 |
点评：本题考查了相似三角形的判定与性质：三角形相似的判定一直是中考考查的热点之一，在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形；或依据基本图形对图形进行分解、组合；或作辅助线构造相似三角形，判定三角形相似的方法有事可单独使用，有时需要综合运用，无论是单独使用还是综合运用，都要具备应有的条件方可．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
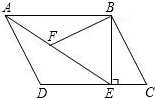如图，在平行四边形ABCD中，过B作BE⊥CD，垂足为点E，连接AE，F为AE上一点，且∠AFB=∠D．
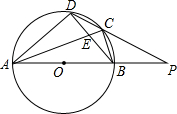如图，四边形ABCD内接于⊙O，AB是⊙O的直径，AC和BD相交于点E，且DC2=CE•CA．
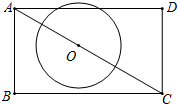如图，已知矩形ABCD中，AB=2，BC=2
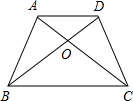如图，在梯形ABCD中，AD∥BC，AD=1，BC=2，若△AOD、△AOB、△BOC的面积分别为S1、S2、S3，则S1：S2：S3=
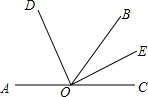如图所示，∠AOB与∠BOC互为补角，OD平分∠AOB，OE平分∠BOC，求∠DOE的度数．
有一个可以自由转动的转盘，被分成了4个相同的扇形，分别标有数1、2、3、4（如图所示），另有一个不透明的口袋装有分别标有数0、1、2的三个小球（除数字不同外，其余都相同）．小亮转动一次转盘，停止后指针指向某一扇形，记下扇形所对应的数，