 如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,点M和点N分别是l1和l2上的动点,MN沿l1和l2平移,若⊙O的半径为1,∠AMN=60°,则下列结论不正确的是( )
如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,点M和点N分别是l1和l2上的动点,MN沿l1和l2平移,若⊙O的半径为1,∠AMN=60°,则下列结论不正确的是( )| A、l1和l2的距离为2 | ||||
B、当MN与⊙O相切时,AM=
| ||||
C、MN=
| ||||
| D、当∠MON=90°时,MN与⊙O相切 |
下列说法中,正确的是( )
| A、90°的圆周角所对的弦是直径 | B、平分弦的直径垂直于弦,并且平分弦所对的两条弧 | C、经过半径的端点并且垂直于这条半径的直线是这个圆的切线 | D、长度相等的弧是等弧 |
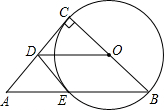 如图,在Rt△ABC中,∠ACB=90°,以BC为直径作圆,交斜边AB于点E,D为AC的中点.连接DO,DE.则下列结论中不一定正确的是( )
如图,在Rt△ABC中,∠ACB=90°,以BC为直径作圆,交斜边AB于点E,D为AC的中点.连接DO,DE.则下列结论中不一定正确的是( )| A、DO∥AB | B、△ADE是等腰三角形 | C、DE⊥AC | D、DE是⊙O的切线 |
用反证法证明“a1,a2,a3,a4,a5都是正数,且a1+a2+a3+a4+a5=1,那么这五个数中至少有一个大于或等于
.”时,应先假设( )
| 1 |
| 5 |
A、这五个数都大于
| ||
B、这五个数都等于
| ||
C、这五个数都小于
| ||
D、这五个数中至少有一个大于或等于
|
用反证法证明“三角形中必有一个角不大于60°”,先假设这个三角形中( )
| A、有一个内角大于60° | B、每一个内角都大于60° | C、有一个内角小于60° | D、至少有一个内角不大于60° |
用反证法证明“△ABC的三个内角中至少有一个内角大于或等于60°”,第一步应假设( )
| A、三角形的三个内角都小于60° | B、三角形的三个内角中至多有一个角大于或等于60° | C、三角形的兰个内角中有两个角大于或等于60° | D、三角形的三个内角都大于或等于60° |
用反证法证明“若实数a,b满足ab=0,则a,b中至少有一个是0”时,应先假设( )
| A、a,b中至多有一个是0 | B、a,b中至少有两个是0 | C、a,b中没有一个是0 | D、a,b都等于0 |
下列命题宜用反证法证明的是( )
| A、等腰三角形两腰上的高相等 | B、有一个外角是1200的等腰三角形是等边三角形 | C、两条直线都与第三条直线平行,则这两条直线互相平行 | D、全等三角形的面积相等 |
在证明“在△ABC中至少有一个角是直角和钝角”时,第一步应假设( )
| A、三角形至少有一个角是直角或钝角 | B、三角形中至少有两个直角或钝角 | C、三角形中没有直角或钝角 | D、三角形中三个角都是直角或钝角 |
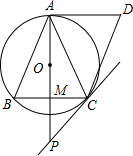 如图,点O是等腰△ABC的外心,AD是圆O的切线,切点为A,过点C作CD≡∥AB,交AD于点D.连接AO并延长交BC于点M,连接AD,交过点C的直线于点P,且∠BCP=∠ACD.
如图,点O是等腰△ABC的外心,AD是圆O的切线,切点为A,过点C作CD≡∥AB,交AD于点D.连接AO并延长交BC于点M,连接AD,交过点C的直线于点P,且∠BCP=∠ACD.