题目内容
10.一系列方程,第1个方程是$x+\frac{x}{2}=3$,解为x=2;第2个方程是 $\frac{x}{2}+\frac{x}{3}=5$,解为x=6;第3个方程是$\frac{x}{3}+\frac{x}{4}=7$,解为x=12;…根据规律第99个方程是$\frac{x}{99}$+$\frac{x}{100}$=199,解为x=9900.分析 根据已知三个方程的特点及解的特点得到一般性规律,即可确定出第99个方程的解.
解答 解:根据题意得到第n个方程为$\frac{x}{n}$+$\frac{x}{n+1}$=2n+1,解为:x=n(n+1)(n为正整数),
则第99个方程是$\frac{x}{99}$+$\frac{x}{100}$=199.
故答案为:$\frac{x}{99}+\frac{x}{100}=199$;x=9900.
点评 此题考查了一元一次方程的解,弄清题中的规律是解本题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
15.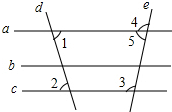 如图,下列说法错误的是( )
如图,下列说法错误的是( )
 如图,下列说法错误的是( )
如图,下列说法错误的是( )| A. | 若∠3=∠2,则b∥c | B. | 若∠3+∠5=180°,则a∥c | ||
| C. | 若∠1=∠2,则a∥c | D. | 若a∥b,b∥c,则a∥c |

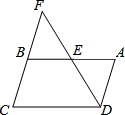 如图,在平行四边形ABCD中,AB=8,AD=6,E是AB上一动点,AE=x,DE的延长线交CB的延长线于点F,设CF=y.
如图,在平行四边形ABCD中,AB=8,AD=6,E是AB上一动点,AE=x,DE的延长线交CB的延长线于点F,设CF=y.