题目内容
18.如图(1),已知∠EAC=90°,∠1+∠2=90,∠1=∠3,∠2=∠4.求证:(1)DE∥BC;
(2)若将图形改变为(2)(3)(4),其他条件不变,(1)的结论是否成立?若成立,请选择一个图形予以证明,不成立,说明理由.

分析 (1)首先证明∠1+∠3+∠2+∠4=180°,进而证明∠D+∠B=180°,即可解决问题.
(2)如图,作辅助线,证明∠AEC+∠ACE+∠3+∠4=180°,即可解决问题.
解答 解:(1)如图1,∵∠1=∠3,∠2=∠4,
∴∠1+∠3+∠2+∠4=2(∠1+∠2),
∵∠1+∠2=90°,
∴∠1+∠3+∠2+∠4=180°;
∵∠D+∠B+∠1+∠3+∠2+∠4=360°,
∴∠D+∠B=180°,
∴DE∥BC.
(2)成立.
如图2,连接EC;
∵∠1=∠3,∠2=∠4,且∠1+∠2=90°,
∴∠3+∠4=∠1+∠2=90°;
∵∠EAC=90°,
∴∠AEC+∠ACE=180°-90°=90°,
∴∠AEC+∠ACE+∠3+∠4=180°,
∴DE∥BC,
即(1)中的结论仍成立.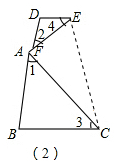
点评 该题考查了平行线的判定问题;解题的关键是灵活运用三角形的内角和定理,结合平行线的判定定理来分析、判断、解答.

练习册系列答案
相关题目
8.已知点(-2,y1),(-3,y2),(1,y3)在函数y=2x2+8x+7的图象上.则y1、y2、y3的大小关系是( )
| A. | y3<y2<y1 | B. | y2<y3<y1 | C. | y1<y2<y3 | D. | y1<y3<y2 |
13.关于($\sqrt{a}$)2与$\sqrt{a^2}$,下列结论中正确的是( )
| A. | a是任意实数时,都有($\sqrt{a}$)2=$\sqrt{a^2}$成立 | B. | 只有a是正数时,才有($\sqrt{a}$)2=$\sqrt{a^2}$成立 | ||
| C. | 当a为有理数时,有($\sqrt{a}$)2=$\sqrt{a^2}$成立 | D. | 当a≥0时,有($\sqrt{a}$)2=$\sqrt{a^2}$成立 |
7.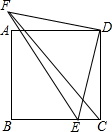 如图,在正方形ABCD中,E是BC上的动点(不与点B、C重合),连接DE,过点D作FD⊥ED于点D,并使FD=ED,连接CF,EF,下列角的大小比较中,一定正确的是( )
如图,在正方形ABCD中,E是BC上的动点(不与点B、C重合),连接DE,过点D作FD⊥ED于点D,并使FD=ED,连接CF,EF,下列角的大小比较中,一定正确的是( )
 如图,在正方形ABCD中,E是BC上的动点(不与点B、C重合),连接DE,过点D作FD⊥ED于点D,并使FD=ED,连接CF,EF,下列角的大小比较中,一定正确的是( )
如图,在正方形ABCD中,E是BC上的动点(不与点B、C重合),连接DE,过点D作FD⊥ED于点D,并使FD=ED,连接CF,EF,下列角的大小比较中,一定正确的是( )| A. | ∠ADF>∠CDE | B. | ∠DCF>∠DFC | C. | ∠DFC>∠ADF | D. | ∠DEC>∠BEF |