题目内容
20．若一个等腰三角形的两边长分别是2和6，此三角形的周长是14，底边是的高是$\sqrt{35}$．分析 分腰长为2和腰长为6两种情况，结合三角形三边关系进行讨论即可求得答案，然后根据勾股定理即可得到底边上的高．
解答 解：当腰长为2时，则三角形三边长为2、2、6，此时2+2＜6，不满足三角形三边关系，故该种情况不存在；
当腰长为6时，则三角形三边长为6、6、2，满足三角形三边关系，此时三角形的周长为6+6+2=14，
综上可知该三角形的周长为14，
底边上的高=$\sqrt{{6}^{2}-{1}^{2}}$=$\sqrt{35}$，
故答案为：14，$\sqrt{35}$．
点评 本题主要考查等腰三角形的性质和三角形三边关系，掌握等腰三角形的两腰相等是解题的关键，注意分类讨论．
练习册系列答案
相关题目
10．
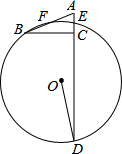如图，△ABC中，AC=5，BC=12，∠ACB=90°，E、F分别为AC、AB中点，过E、F两点作⊙O，延长AC交⊙O于D，若∠CDO=$\frac{1}{2}$∠B，则⊙O的半径为（ ）
如图，△ABC中，AC=5，BC=12，∠ACB=90°，E、F分别为AC、AB中点，过E、F两点作⊙O，延长AC交⊙O于D，若∠CDO=$\frac{1}{2}$∠B，则⊙O的半径为（ ）| A． | 13 | B． | $2\sqrt{26}$ | C． | $3\sqrt{26}$ | D． | $\frac{27}{2}$ |
11．某公司生产的A种产品，每件成本是2元，每件售价是3元，一年的销售量是10万件．为了获得更多的利润，公司准备拿出一定资金来做广告．根据经验，每年投入的广告费为x（万元）时，产品的年销售量是原来的y倍，且y是x的二次函数，公司作了预测，知x与y之间的对应关系如表：
（1）根据表中，求y关于x的函数关系式；
（2）如果把利润看成是销售总额减去成本和广告费，请你写出年利润S（万元）与广告费x（万元）的函数关系式；
（3）根据上面的函数关系式，你认为每年投入多少广告费最合适？为什么？
| x（万元） | 0 | 1 | 2 | … |
| y | 1 | 1.5 | 1.8 | … |
（2）如果把利润看成是销售总额减去成本和广告费，请你写出年利润S（万元）与广告费x（万元）的函数关系式；
（3）根据上面的函数关系式，你认为每年投入多少广告费最合适？为什么？
8．已知点（-2，y1），（-3，y2），（1，y3）在函数y=2x2+8x+7的图象上．则y1、y2、y3的大小关系是（ ）
| A． | y3＜y2＜y1 | B． | y2＜y3＜y1 | C． | y1＜y2＜y3 | D． | y1＜y3＜y2 |
15．在-1，0，-2，1这四个数中，最大的数是（ ）
| A． | -4 | B． | -2 | C． | 0 | D． | 1 |
如图，∠1和∠3是直线a、b被直线c所截得到的同旁内角；
12．
如图，直线AB、CD相交于点O，OA平分∠EOC，∠EOC=70°，则∠BOD的度数等于（ ）
如图，直线AB、CD相交于点O，OA平分∠EOC，∠EOC=70°，则∠BOD的度数等于（ ）| A． | 20° | B． | 30° | C． | 35° | D． | 40° |