题目内容
1．有若干块长方形和正方形纸片如图所示，用若干块这样的硬纸片拼成一个新的长方形．（1）用两种不同方法计算图（2）中长方形的面积，由此可得出一个等式．
（2）有若干块如图（3）所示的B型长方形和A、C型正方形硬纸片
①小明想用拼图的方法解释多项式乘法（3a+2b）（a+b）=3a2+5ab+2b2，那么需要A型卡片3张，B型卡片5张．
②试借助拼图的方法，把二次三项式a2+4ab+3b2因式分解；画出拼图，并写出因式分解的结果．
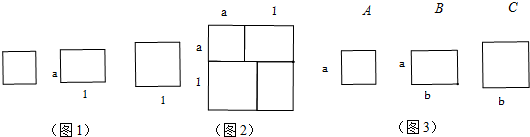
分析 （1）分别写出边长为（a+1）的面积和由4个矩形所组成的正方形的面积即可得到完全平方公式；
（2）由（3a+2b）（a+b）=3a2+5ab+2b2得到边长为3a+b和a+b的矩形由A型卡片3张，B型卡片5张，C型卡片2张组成；
（3）先分解因式，于是可判断边长为a+b和a+3b的矩形由A型卡片1张，B型卡片4张，C型卡片3张组成．
解答 解：（1）（a+1）2=a2+2a+1；
（2）需要A型卡片3张，B型卡片5张；
故答案为3，5；
（3）a2+4ab+3b2=（a+3b）（a+b）．
如图，
点评 本题考查了因式分解的应用：利用因式分解解决求值问题；利用因式分解解决证明问题；利用因式分解简化计算问题．
练习册系列答案
优学名师名题系列答案
相关题目
11．某公司生产的A种产品，每件成本是2元，每件售价是3元，一年的销售量是10万件．为了获得更多的利润，公司准备拿出一定资金来做广告．根据经验，每年投入的广告费为x（万元）时，产品的年销售量是原来的y倍，且y是x的二次函数，公司作了预测，知x与y之间的对应关系如表：
（1）根据表中，求y关于x的函数关系式；
（2）如果把利润看成是销售总额减去成本和广告费，请你写出年利润S（万元）与广告费x（万元）的函数关系式；
（3）根据上面的函数关系式，你认为每年投入多少广告费最合适？为什么？
| x（万元） | 0 | 1 | 2 | … |
| y | 1 | 1.5 | 1.8 | … |
（2）如果把利润看成是销售总额减去成本和广告费，请你写出年利润S（万元）与广告费x（万元）的函数关系式；
（3）根据上面的函数关系式，你认为每年投入多少广告费最合适？为什么？
12．
如图，直线AB、CD相交于点O，OA平分∠EOC，∠EOC=70°，则∠BOD的度数等于（ ）
如图，直线AB、CD相交于点O，OA平分∠EOC，∠EOC=70°，则∠BOD的度数等于（ ）| A． | 20° | B． | 30° | C． | 35° | D． | 40° |
13．关于（$\sqrt{a}$）2与$\sqrt{a^2}$，下列结论中正确的是（ ）
| A． | a是任意实数时，都有（$\sqrt{a}$）2=$\sqrt{a^2}$成立 | B． | 只有a是正数时，才有（$\sqrt{a}$）2=$\sqrt{a^2}$成立 | ||
| C． | 当a为有理数时，有（$\sqrt{a}$）2=$\sqrt{a^2}$成立 | D． | 当a≥0时，有（$\sqrt{a}$）2=$\sqrt{a^2}$成立 |