题目内容
11. 某数学兴趣小组对函数y=x+$\frac{1}{x}$的图象和性质进行了探究,探究过程如下,请补充完整.
某数学兴趣小组对函数y=x+$\frac{1}{x}$的图象和性质进行了探究,探究过程如下,请补充完整.| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | -$\frac{10}{3}$ | m | -2 | -$\frac{5}{2}$ | -$\frac{10}{3}$ | $\frac{10}{3}$ | $\frac{5}{2}$ | 2 | $\frac{5}{2}$ | $\frac{10}{3}$ | … |
(2)根据(1)中表内的数据,在如图所示的平面直角坐标系中描点,画出函数图象的一部分,请你画出该函数图象的另一部分.
(3)请你根据函数图象,写出两条该函数的性质;
(4)进一步探究该函数的图象发现:
①方程x+$\frac{1}{x}$=3有2个实数根;
②若关于x的方程x+$\frac{1}{x}$=t有2个实数根,则t的取值范围是t<-2或t>2.
分析 (1)由x在分母上,即可得出自变量x的取值范围是x≠0,将x=-2代入函数关系式中即可求出m值;
(2)描点、连线,补充函数图象;
(3)观察函数图象,随便找出两条该函数的性质即可;
(4)①观察函数图象,由函数y=x+$\frac{1}{x}$的图象与直线y=3的交点的个数,可得出结论;
②观察函数图象,找出当t<-2或t>2时,函数y=x+$\frac{1}{x}$的图象与直线y=t有两个交点,此题得解.
解答 解:(1)∵x在分母上,
∴x≠0.
当x=-2时,m=y=-2+$\frac{1}{-2}$=-$\frac{5}{2}$.
故答案为:x≠0;-$\frac{5}{2}$.
(2)描点、连线,画出函数图象,如图所示.
(3)观察函数图象,可找出函数性质:
①函数图象关于原点中心对称;②当x>1时,y的值随x值的增大而增大.
(4)①方程x+$\frac{1}{x}$=3可看成函数y=x+$\frac{1}{x}$的图象与直线y=3的交点的个数,
∵函数y=x+$\frac{1}{x}$的图象与直线y=3有两个交点,
∴方程x+$\frac{1}{x}$=3有2个实数根.
故答案为:2.
②观察函数图象可知,当t<-2或t>2时,函数y=x+$\frac{1}{x}$的图象与直线y=t有两个交点.
故答案为:t<-2或t>2.
点评 本题考查了反比例函数的性质、一次函数的图象、一次函数的性质以及反比例函数的图象,解题的关键是:(1)由x在分母上找出x的取值范围;(2)描点、连线,补充函数图象;(3)观察函数图象,找出该函数的性质;(4)①由函数y=x+$\frac{1}{x}$的图象与直线y=3有两个交点得出结论;②观察函数图象,找出结论.

练习册系列答案
相关题目
19.下列方程中不是二项方程的是( )
| A. | x2+x=0 | B. | $\frac{1}{3}{x}^{2}$+9=0 | C. | x5=1 | D. | 2-x4=3 |
16.下列各式成立的是( )
| A. | $\sqrt{{{({-2})}^2}}=-2$ | B. | $\sqrt{{{({-3})}^2}}=9$ | C. | $\sqrt{x^2}=x$ | D. | $\sqrt{{{({-5})}^2}}=5$ |
3. 在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表
请根据以上信息解答下列问题:
(1)求m,n的值;
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在哪一组?
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.
 在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表
| 组别 | 步数分组 | 频数 |
| A | 5500≤x<6500 | 2 |
| B | 6500≤x<7500 | 10 |
| C | 7500≤x<8500 | m |
| D | 8500≤x<9500 | 3 |
| E | 9500≤x<10500 | n |
(1)求m,n的值;
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在哪一组?
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.

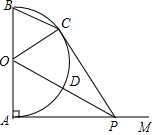 如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC.
如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC. 如图所示,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若△ABC的周长为10cm,则△OEC的周长为5cm.
如图所示,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若△ABC的周长为10cm,则△OEC的周长为5cm.