题目内容
20.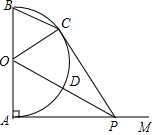 如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC.
如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC.(1)求证:△OAP≌△OCP;
(2)若半圆O的半径等于2,填空:
①当AP=2时,四边形OAPC是正方形;
②当AP=2$\sqrt{3}$时,四边形BODC是菱形.
分析 (1)根据切线的性质,可以得到OP⊥AC,然后利用“HL”证明:△OAP≌△OCP;
(2)①根据正方形的性质可以得到AP的长;
②先利用菱形的性质得到△OBC为等边三角形,则∠B=60°,所以∠AOP=60°,然后在Rt△OAP中利用正切的定义求AP即可.
解答 (1)证明:∵PC切半圆O于点C,
∴OC⊥PC,
∵AM⊥AB,
∴∠OAP=90°,
在Rt△OAP和Rt△OCP中
$\left\{\begin{array}{l}{OP=OP}\\{OA=OC}\end{array}\right.$,
∴Rt△OAP≌Rt△OCP;
(2)解:①∵Rt△OAP≌Rt△OCP,
∴PA=PC,
而OA=OC,
∴当AO=AP时,四边形OAPC为菱形,
而∠OAP=90°,
∴四边形OAPC是正方形,
此时AP=OA=2;
②∵四边形BODC是菱形,
∴OB=OD=CD=BC,BC∥OD,
∴△OBC为等边三角形,
∴∠B=60°,
∴∠AOP=60°,
在Rt△OAP中,∵tan∠AOP=$\frac{AP}{OA}$,
∴AP=2tan60°=2$\sqrt{3}$,
即AP=2$\sqrt{3}$时,四边形BODC是菱形.
故答案为2,2$\sqrt{3}$.
点评 本题考查了圆的综合题:熟练掌握切线的性质、菱形和正方形的判定方法;会灵活利用全等三角形的判定方法证明两三角形全等.

练习册系列答案
相关题目
10. 如图,在方格纸中,△ABC经过变换得到△DEF,正确的变换是( )
如图,在方格纸中,△ABC经过变换得到△DEF,正确的变换是( )
 如图,在方格纸中,△ABC经过变换得到△DEF,正确的变换是( )
如图,在方格纸中,△ABC经过变换得到△DEF,正确的变换是( )| A. | 把△ABC向下平移4格,再绕点C逆时针方向旋转180° | |
| B. | 把△ABC向下平移5格,再绕点C顺时针方向旋转180° | |
| C. | 把△ABC绕点C逆时针方向旋转90°,再向下平移2格 | |
| D. | 把△ABC绕点C顺时针方向旋转90°,再向下平移5格 |
11. 某数学兴趣小组对函数y=x+$\frac{1}{x}$的图象和性质进行了探究,探究过程如下,请补充完整.
某数学兴趣小组对函数y=x+$\frac{1}{x}$的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是x≠0,m=-$\frac{5}{2}$.
(2)根据(1)中表内的数据,在如图所示的平面直角坐标系中描点,画出函数图象的一部分,请你画出该函数图象的另一部分.
(3)请你根据函数图象,写出两条该函数的性质;
(4)进一步探究该函数的图象发现:
①方程x+$\frac{1}{x}$=3有2个实数根;
②若关于x的方程x+$\frac{1}{x}$=t有2个实数根,则t的取值范围是t<-2或t>2.
 某数学兴趣小组对函数y=x+$\frac{1}{x}$的图象和性质进行了探究,探究过程如下,请补充完整.
某数学兴趣小组对函数y=x+$\frac{1}{x}$的图象和性质进行了探究,探究过程如下,请补充完整.| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | -$\frac{10}{3}$ | m | -2 | -$\frac{5}{2}$ | -$\frac{10}{3}$ | $\frac{10}{3}$ | $\frac{5}{2}$ | 2 | $\frac{5}{2}$ | $\frac{10}{3}$ | … |
(2)根据(1)中表内的数据,在如图所示的平面直角坐标系中描点,画出函数图象的一部分,请你画出该函数图象的另一部分.
(3)请你根据函数图象,写出两条该函数的性质;
(4)进一步探究该函数的图象发现:
①方程x+$\frac{1}{x}$=3有2个实数根;
②若关于x的方程x+$\frac{1}{x}$=t有2个实数根,则t的取值范围是t<-2或t>2.
5.公交公司的某路公交车每月运营总支出的费用为4000元,乘客乘车的票价为2元/人次.设每月的乘客量为x(人次),每月的赢利额为y(元).(赢利额=总收入-总支出)
(1)y(元)与x(人次)之间的关系式为y=2x-4000;(x为正整数)
(2)根据关系式填表:
(3)根据表格数据,当月乘客量超过2000人次时,该路公交车运营才能赢利.
(1)y(元)与x(人次)之间的关系式为y=2x-4000;(x为正整数)
(2)根据关系式填表:
| x/人次 | 500 | 1000 | 1500 | 2000 | 2500 | 3000 |
| y/元 | -3000 | -2000 | -1000 | 0 | 1000 | 2000 |
 如图,甲乙两人在游泳池A处发现游泳池中的P处有人求救,甲立即跳入池中去救人,速度为1米/秒,乙以3.5米/秒的速度沿游泳池边跑到距A不远处的B处,捡起一个游泳圈再跳入池中去救人,甲游了20秒到达P处,两秒后乙到达P处.若∠PAB与∠PBC互余,且cos∠PBC=$\frac{3}{5}$,求乙的游泳速度.
如图,甲乙两人在游泳池A处发现游泳池中的P处有人求救,甲立即跳入池中去救人,速度为1米/秒,乙以3.5米/秒的速度沿游泳池边跑到距A不远处的B处,捡起一个游泳圈再跳入池中去救人,甲游了20秒到达P处,两秒后乙到达P处.若∠PAB与∠PBC互余,且cos∠PBC=$\frac{3}{5}$,求乙的游泳速度. 如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为弧BD的中点,若∠DAB=40°,则∠ABC=70°.
如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为弧BD的中点,若∠DAB=40°,则∠ABC=70°.