��Ŀ����
3�� Сѧ�������Ѿ�ѧ�������ε������ڽǺ͵���180�㣬������һ��֤����A+��B+��C=180��ķ����������˵�����̣���գ�����ͼ����������ABC��һ��BC��ȡһ��D��DE��AC��DF��AB����Ϊ˵�����㣬ͳһ��ע�����ֱ�ʾ�Ľǣ���
Сѧ�������Ѿ�ѧ�������ε������ڽǺ͵���180�㣬������һ��֤����A+��B+��C=180��ķ����������˵�����̣���գ�����ͼ����������ABC��һ��BC��ȡһ��D��DE��AC��DF��AB����Ϊ˵�����㣬ͳһ��ע�����ֱ�ʾ�Ľǣ�����DE��AC����֪����
���C=��1��������ֱ��ƽ�У�ͬλ����ȣ�
�֡�DE��AC����֪�����á�2=��4�����ݸ�����ֱ��ƽ�У��ڴ�����ȣ�
��DF��AB����֪�������B=��3��������ֱ��ƽ�У�ͬλ����ȣ�
�֡�DF��AB����֪�������A=��DFC��������ֱ��ƽ�У�ͬλ����ȣ�
�ߡ�A+��B+��C=��DFC+��3+��1������������õ���������
�֡�2=��4�����A+��B+��C=��2+��3+��1=180�㣬���ݸ���ƽ�ǵĶ��壮
���� ������ֱ��ƽ�У�ͬλ����ȿɵá�1=��B����3=��C����4=��A���ٸ�����ֱ��ƽ�У��ڴ�����ȿɵá�2=��4���Ӷ���֤��
��� �⣺ ��DE��AC����֪����
��DE��AC����֪����
���C=��1��������ֱ��ƽ�У�ͬλ����ȣ�
�֡�DE��AC����֪�����á�2=��4��������ֱ��ƽ�У��ڴ�����ȣ�
��DF��AB����֪�������B=��3��������ֱ��ƽ�У�ͬλ����ȣ�
�֡�DF��AB����֪�������A=��DFC��������ֱ��ƽ�У�ͬλ����ȣ�
�ߡ�A+��B+��C=��DFC+��3+��1������������õ���������
�֡�2=��4�����A+��B+��C=��2+��3+��1=180�㣬����ƽ�ǵĶ��壮
�ʴ�Ϊ��1����ֱ��ƽ�У�ͬλ����ȣ���ֱ��ƽ�У�3����ֱ��ƽ�У��ڴ�����ȣ�DFC����ֱ��ƽ�У�ͬλ����ȣ���ֱ��ƽ�У�ͬλ����ȣ�DFC��3��1��2��3��1������ƽ�ǵĶ��壮
���� ���⿼����ƽ���ߵ����ʣ��Ƚϼ���������ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ������ҵ��ͬ����ϰ��ϵ�д�
������ҵ��ͬ����ϰ��ϵ�д� С��ſ�ʱ��ҵϵ�д�
С��ſ�ʱ��ҵϵ�д� һ������ϵ�д�
һ������ϵ�д� �Ƹ�С״Ԫ���ֳ������ϵ�д�
�Ƹ�С״Ԫ���ֳ������ϵ�д�
�����Ŀ
14������x+3����x+n��=x2+mx-15����m��ֵΪ��������
| A�� | -5 | B�� | -2 | C�� | 5 | D�� | 2 |
11����������ʵ��x�����и�ʽ��һ���������ǣ�������
| A�� | $\sqrt{{x}^{2}-1}$=$\sqrt{x-1}$•$\sqrt{x+1}$ | B�� | $\sqrt{{��x+1��}^{2}}$=x+1 | C�� | $\sqrt{��-4��•��-x��}$=$\sqrt{-4}$•$\sqrt{-x}$ | D�� | $\sqrt{3{6x}^{4}}$=6x2 |
18�� ij������ʽ��Ľ⼯�������ϱ�ʾ��ͼ�����������ʽ������ǣ�������
ij������ʽ��Ľ⼯�������ϱ�ʾ��ͼ�����������ʽ������ǣ�������
 ij������ʽ��Ľ⼯�������ϱ�ʾ��ͼ�����������ʽ������ǣ�������
ij������ʽ��Ľ⼯�������ϱ�ʾ��ͼ�����������ʽ������ǣ�������| A�� | $\left\{\begin{array}{l}{x��5}\\{x��1}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x��5}\\{x��-1}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{x��5}\\{x��-1}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x��5}\\{x��-1}\end{array}\right.$ |
15������ʽ4+2x��0�Ľ⼯�ǣ�������
| A�� | 2x��4 | B�� | x��2 | C�� | x��-2 | D�� | x��-2 |
 ��ͼ���ı���ABCD�����Σ�AC=8��DB=6��DH��AB�ڵ�H������OH��
��ͼ���ı���ABCD�����Σ�AC=8��DB=6��DH��AB�ڵ�H������OH�� ��ͼ����?ABCD�У���D=45�㣬��CAD=35�㣬���B�͡�BAC�Ķ�����
��ͼ����?ABCD�У���D=45�㣬��CAD=35�㣬���B�͡�BAC�Ķ�����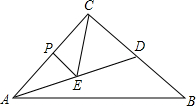 ��ͼ����Rt��ABC�У���C=90�㣬AC=4��BC=5��D��BC����һ�㣬CD=3��P��AC����һ���㣨����A��C�غϣ�������P��PE��BC��AD�ڵ�E������ABD��ֱ��AD���ۣ��õ���AB��D������B��C������ACE=��BCB��ʱ����AE=$\frac{64}{25}$��
��ͼ����Rt��ABC�У���C=90�㣬AC=4��BC=5��D��BC����һ�㣬CD=3��P��AC����һ���㣨����A��C�غϣ�������P��PE��BC��AD�ڵ�E������ABD��ֱ��AD���ۣ��õ���AB��D������B��C������ACE=��BCB��ʱ����AE=$\frac{64}{25}$��