题目内容
13.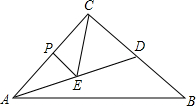 如图,在Rt△ABC中,∠C=90°,AC=4,BC=5,D是BC边上一点,CD=3,P是AC边上一动点(不与A、C重合),过点P作PE∥BC交AD于点E,将△ABD沿直线AD翻折,得到△AB′D,连接B′C,当∠ACE=∠BCB′时,则AE=$\frac{64}{25}$.
如图,在Rt△ABC中,∠C=90°,AC=4,BC=5,D是BC边上一点,CD=3,P是AC边上一动点(不与A、C重合),过点P作PE∥BC交AD于点E,将△ABD沿直线AD翻折,得到△AB′D,连接B′C,当∠ACE=∠BCB′时,则AE=$\frac{64}{25}$.
分析 延长AD交BB′于F,则AF⊥BB′,证明△ACD∽△BFD,求出BF的长,得到BB′的长,证明△ACE∽△BCB′,根据相似三角形的性质计算即可.
解答 解: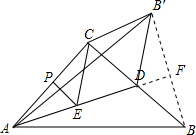 延长AD交BB′于F,则AF⊥BB′,
延长AD交BB′于F,则AF⊥BB′,
则∠ACD=∠BFD,
∵∠ADC=∠FDB,
∴∠CAD=∠FBD,
∴△ACD∽△BFD,
∴$\frac{BF}{AC}$=$\frac{BD}{AD}$,即$\frac{BF}{4}$=$\frac{2}{5}$,
∴BF=$\frac{8}{5}$,
∴BB′=$\frac{16}{5}$,
∵∠ACE=∠BCB′,∠CAE=∠CBB′,
∴△ACE∽△BCB′,
∴AE=$\frac{64}{25}$.
故答案为:$\frac{64}{25}$.
点评 本题考查了相似三角形的判定与性质、翻折变换的性质,掌握相似三角形的判定定理和性质定理、理解折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.

练习册系列答案
相关题目
 小学里我们已经学过三角形的三个内角和等于180°,下面是一种证明∠A+∠B+∠C=180°的方法,请完成说理过程(填空):如图,在三角形ABC的一边BC上取一点D,DE∥AC,DF∥AB.(为说理方便,统一标注了数字表示的角).
小学里我们已经学过三角形的三个内角和等于180°,下面是一种证明∠A+∠B+∠C=180°的方法,请完成说理过程(填空):如图,在三角形ABC的一边BC上取一点D,DE∥AC,DF∥AB.(为说理方便,统一标注了数字表示的角).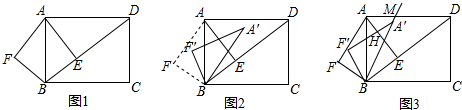
 如图,AB∥EF∥CD,点P在线段EF上,当点P从E向F沿线段EF移动时,∠A,∠APC,∠C之间有什么关系?
如图,AB∥EF∥CD,点P在线段EF上,当点P从E向F沿线段EF移动时,∠A,∠APC,∠C之间有什么关系?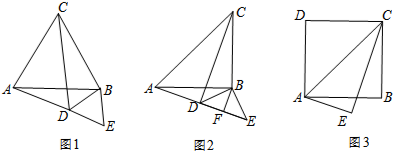
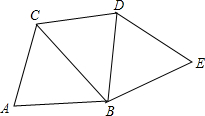 如图,将△ABC沿BC折叠得到△BCD,再将△BCD沿BD折叠得到△BDE,设折叠后所得多边形的边数为n.
如图,将△ABC沿BC折叠得到△BCD,再将△BCD沿BD折叠得到△BDE,设折叠后所得多边形的边数为n.
 如图,矩形纸片ABCD中,AB=6cm,AD=10cm,点E、F在矩形ABCD的边AB、AD上运动,将△AEF沿EF折叠,使点A′在BC边上,当折痕EF移动时,点A′在BC边上也随之移动.则A′C的取值范围为4cm≤A′C≤8cm.
如图,矩形纸片ABCD中,AB=6cm,AD=10cm,点E、F在矩形ABCD的边AB、AD上运动,将△AEF沿EF折叠,使点A′在BC边上,当折痕EF移动时,点A′在BC边上也随之移动.则A′C的取值范围为4cm≤A′C≤8cm.