题目内容
11．对于任意实数x，下列各式中一定成立的是（ ）| A． | $\sqrt{{x}^{2}-1}$=$\sqrt{x-1}$•$\sqrt{x+1}$ | B． | $\sqrt{{（x+1）}^{2}}$=x+1 | C． | $\sqrt{（-4）•（-x）}$=$\sqrt{-4}$•$\sqrt{-x}$ | D． | $\sqrt{3{6x}^{4}}$=6x2 |
分析 根据二次根式的乘除法法则和二次根式的性质进行判断即可．
解答 解：当x≥1时，$\sqrt{{x}^{2}-1}=\sqrt{x+1}•\sqrt{x-1}$，A错误；
当x≥-1时，$\sqrt{（x+1）^{2}}$=x+1，B错误；
$\sqrt{（-4）（-x）}$=$\sqrt{-4}$•$\sqrt{-x}$，C错误；
$\sqrt{36{x}^{4}}$=6x2，D正确．
故选：D．
点评 本题考查的是二次根式的乘除法、二次根式的化简，掌握二次根式的乘除法法则和二次根式的性质是解题的关键．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
1．
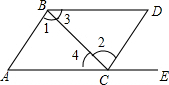如图所示，点E在AC的延长线上，下列条件中不能判断BD∥AE的是（ ）
如图所示，点E在AC的延长线上，下列条件中不能判断BD∥AE的是（ ）| A． | ∠1=∠2 | B． | ∠D+∠ACD=180° | C． | ∠D=∠DCE | D． | ∠3=∠4 |
如图，已知∠1=∠2，∠3+∠4=180°，证明AB∥EF．
16．在下列实数中，无理数是（ ）
| A． | 0 | B． | -$\frac{22}{7}$ | C． | $\sqrt{2}$ | D． | $\sqrt{9}$ |
小学里我们已经学过三角形的三个内角和等于180°，下面是一种证明∠A+∠B+∠C=180°的方法，请完成说理过程（填空）：如图，在三角形ABC的一边BC上取一点D，DE∥AC，DF∥AB．（为说理方便，统一标注了数字表示的角）．