题目内容
4．若a、b、c表示一个三角形的三条边的长，则多项式a2-（b+c）2的值一定（ ）| A． | 大于0 | B． | 小于0 | C． | 等于0 | D． | 无法确定 |
分析 根据三角形三边关系，即可得到0＜a＜b+c，可得a2＜（b+c）2，据此可得a2-（b+c）2的值一定小于0．
解答 解：∵a、b、c表示一个三角形的三条边的长，
∴0＜a＜b+c，
∴a2＜（b+c）2，
∴a2-（b+c）2的值一定小于0，
故选：B．
点评 本题主要考查了三角形的三边关系，解题时注意：三角形两边之和大于第三边．
练习册系列答案
相关题目
如图，已知线段AB=5，延长线段AB到C，使BC=2AB．
13．下列两个不等式的解集完全相同的是（ ）
| A． | -4x＜24与x＜-6 | B． | 3x≤9与x-3≥0 | ||
| C． | 2x-7＜6x与x＜-$\frac{7}{4}$ | D． | -$\frac{1}{2}$x+3＜0与$\frac{1}{3}$x-2＞0 |
20．已知：关于x方程$\frac{x}{x+1}$+$\frac{x+1}{x}$=$\frac{4x+k}{{x}^{2}+x}$有且仅有一个实数根，则k的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{2}$或1 | C． | $\frac{1}{2}$或5或1 | D． | $\frac{1}{2}$或5或-2 |
16．若$\sqrt{{（2a+4）}^{2}}$=2a+4，则a的取值范围为（ ）
| A． | a≥2 | B． | a≤2 | C． | a≥-2 | D． | a≤-2 |
13．
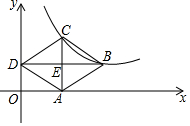如图，菱形ABCD的顶点A在x轴上，D在y轴上，B、C在反比例函数的图象上，对角线AC、BD交于点E，且BD∥x轴，若AE=1，∠ADE=30°，则反比例函数的表达式为（ ）
如图，菱形ABCD的顶点A在x轴上，D在y轴上，B、C在反比例函数的图象上，对角线AC、BD交于点E，且BD∥x轴，若AE=1，∠ADE=30°，则反比例函数的表达式为（ ）| A． | $y=\frac{2}{x}$ | B． | $y=\frac{3}{x}$ | C． | $y=\frac{{\sqrt{3}}}{x}$ | D． | $y=\frac{{2\sqrt{3}}}{x}$ |