题目内容
13.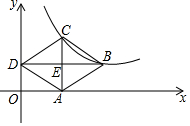 如图,菱形ABCD的顶点A在x轴上,D在y轴上,B、C在反比例函数的图象上,对角线AC、BD交于点E,且BD∥x轴,若AE=1,∠ADE=30°,则反比例函数的表达式为( )
如图,菱形ABCD的顶点A在x轴上,D在y轴上,B、C在反比例函数的图象上,对角线AC、BD交于点E,且BD∥x轴,若AE=1,∠ADE=30°,则反比例函数的表达式为( )| A. | $y=\frac{2}{x}$ | B. | $y=\frac{3}{x}$ | C. | $y=\frac{{\sqrt{3}}}{x}$ | D. | $y=\frac{{2\sqrt{3}}}{x}$ |
分析 直接利用菱形的性质结合已知得出C点坐标,进而得出反比例函数的表达式.
解答 解:∵菱形ABCD的顶点A在x轴上,AE=1,∠ADE=30°,
∴AD=2,则DE=$\sqrt{3}$,
故AC=2,则C点坐标为:($\sqrt{3}$,2),
故反比例函数的表达式为:y=$\frac{2\sqrt{3}}{x}$.
故选:D.
点评 此题主要考查了菱形的性质以及反比例函数图象上点的坐标性质,正确得出C点坐标是解题关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
4.若a、b、c表示一个三角形的三条边的长,则多项式a2-(b+c)2的值一定( )
| A. | 大于0 | B. | 小于0 | C. | 等于0 | D. | 无法确定 |
18.如果直角三角形的边长为3,4,a,则a的值是( )
| A. | 5 | B. | 6 | C. | $\sqrt{7}$ | D. | 5或$\sqrt{7}$ |
 2016年1月的日期排列成如图数表,用十字框框出5个数(如图所示).
2016年1月的日期排列成如图数表,用十字框框出5个数(如图所示).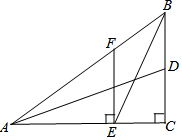 如图△ABC中,∠ACB=90°,AB=10,BC=6,AC=8,BE是∠ABC的角平分线,AD是BC边的中线,EF⊥AC于点E,下列结论正确的有( )个
如图△ABC中,∠ACB=90°,AB=10,BC=6,AC=8,BE是∠ABC的角平分线,AD是BC边的中线,EF⊥AC于点E,下列结论正确的有( )个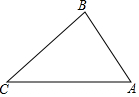 如图,在△ABC中,∠C=45°,∠B=75°,BC=$\sqrt{6}$,求AB的长.
如图,在△ABC中,∠C=45°,∠B=75°,BC=$\sqrt{6}$,求AB的长. 如图,A、B两点被池塘隔开,请你运用所学知识,说说怎样测出A、B两点间的距离?根据是什么?
如图,A、B两点被池塘隔开,请你运用所学知识,说说怎样测出A、B两点间的距离?根据是什么?