题目内容
14.“五水共治,保护母亲河”在丽水城区治理河道工程中需租用甲、乙两车清理淤泥.据估算,单独租用乙车完成任务比单独租用甲车完成任务多用15天,且甲车的工作效率是乙车工作效率的2倍.(1)甲、乙两车单独完成任务分别需要多少天?
(2)已知两车合运完成任务共需租金32500元,甲车每天的租金比乙车每天的租金多750元,请选择一种租金最少的租车方案(可租一辆或两辆)并说明理由.
分析 (1)设甲车单独完成认为需要x天,则乙车单独完成需要2x天,根据“单独租用乙车完成任务比单独租用甲车完成任务多用15天”列出方程并解答;
(2)根据题意和第(1)问中的结果可以分别求得三种方式的费用,从而可以解答本题.
解答 解:(1)设甲车单独完成认为需要x天,则乙车单独完成需要2x天,
依题意得:2x-x=15,
解得x=15.
则2x=30.
答:甲车单独完成认为需要15天,则乙车单独完成需要30天;
(2)甲、乙两车合作时需要工作的时间为:$\frac{1}{\frac{1}{15}+\frac{1}{30}}$=10(天)
设甲车的租金每天a元,则乙车的租金每天(a-750)元,
[a+(a-750)]×10=32500
解得,a=2000
∴a-750=1250
当单独租甲车时,租金为:15×2000=30000,
当单独租乙车时,租金为:30×1250=37500,
∵30000<32500<37500,
∴单独租甲车租金最少.
点评 本题考查了一元一次方程的应用和一元一次不等式的应用.解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
4.若a、b、c表示一个三角形的三条边的长,则多项式a2-(b+c)2的值一定( )
| A. | 大于0 | B. | 小于0 | C. | 等于0 | D. | 无法确定 |
19.A、B两店以同样价格出售一种商品,并推出不同的优惠方案;在A店累计购物超过100元后,超出100元的部分打9折;在B店累计购物超过50元后,超出50元的部分打9.5折,则顾客到两店购物花费一样时为( )
| A. | 累计购物不超过50元 | |
| B. | 累计购物超过50元而不超过100元 | |
| C. | 累计购物超过100元 | |
| D. | 累计购物不超过50元或刚好为150元 |
 如图,A、B两点被池塘隔开,请你运用所学知识,说说怎样测出A、B两点间的距离?根据是什么?
如图,A、B两点被池塘隔开,请你运用所学知识,说说怎样测出A、B两点间的距离?根据是什么?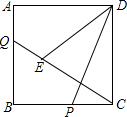 如图,四边形ABCD为正方形,AD=3,点P、点Q分别是BC、AB边上的动点,CP=AQ,连接DP、CQ,在线段CQ上有一动点E,满足∠DEC=∠DPC,则CE•CQ的值为9.
如图,四边形ABCD为正方形,AD=3,点P、点Q分别是BC、AB边上的动点,CP=AQ,连接DP、CQ,在线段CQ上有一动点E,满足∠DEC=∠DPC,则CE•CQ的值为9. 如图,点D、E分别为△ABC的边BC、CA上的点,且BD:CD=1:1,AE:CE=2:3,AD与BE相交于点F,则AF:DF=4:3.
如图,点D、E分别为△ABC的边BC、CA上的点,且BD:CD=1:1,AE:CE=2:3,AD与BE相交于点F,则AF:DF=4:3.