Question

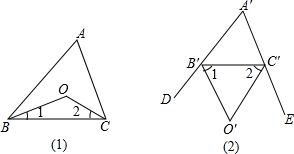
如图（1），在△ABC中，∠ABC、∠ACB的平分线相交于点O
（a）若∠A=60°，求∠BOC的度数；
（b）若∠A=n°，则∠BOC=

 

；
（c）若∠BOC=3∠A，则∠A=

 

；
（2）如图（2），在△A′B′C′中的外角平分线相交于点O′，∠A′=40°，求∠B′O′C′的度数；
（3）上面（1），（2）两题中的∠BOC与∠B′O′C′有怎样的数量关系？

Answer 1

考点：三角形内角和定理

专题：

分析：（1）（a）根据角平分线的定义可得∠1=

1

2

∠ABC，∠2=

1

2

∠ACB，然后求出∠1+∠2的值，再根据三角形的内角和等于180°可得出结论；
（b）同（a）的证明过程；
（c）根据角平分线的定义用∠A表示出∠1+∠2的值，再由∠BOC=3∠A即可得出结论；
（2）先求出∠A的外角的度数，由三角形的外角和等于360°及角平分线的性质得出∠1+∠2的度数，再由三角形内角和定理即可得出结论；
（3）根据（1）（2）中∠BOC与∠B′O′C′的关系可得出结论．

解答： 解：（1）（a）∵∠ABC、∠ACB的平分线相交于点O，
∴∠1=

1

2

∠ABC，∠2=

1

2

∠ACB，
∴∠1+∠2=

1

2

（∠ABC+∠ACB）=

1

2

（180°-∠A）=

1

2

×（180°-60°）=60°，
∴∠BOC=180°-60°=120°；
（b））∵∠ABC、∠ACB的平分线相交于点O，
∴∠1=

1

2

∠ABC，∠2=

1

2

∠ACB，
∴∠1+∠2=

1

2

（∠ABC+∠ACB）=

1

2

（180°-∠A）=

1

2

×（180°-n°）=90°-

1

2

n°，
∴∠BOC=180°-（90°-

1

2

n°）=90°+

1

2

n°．
故答案为：90°+

1

2

n°；
（c）∵∠ABC、∠ACB的平分线相交于点O，∠BOC=3∠A，
∴∠1=

1

2

∠ABC，∠2=

1

2

∠ACB，
∴∠1+∠2=

1

2

（∠ABC+∠ACB）=

1

2

（180°-∠A）=90°-

1

2

∠A，
∴90°-

1

2

∠A+3∠A=180°，解得∠A=36°
故答案为：36°；

（2）∵∠A=40°，
∴∠A的外角等于180°-40°=140°，
∵△A′B′C′另外的两外角平分线相交于点O′，三角形的外角和等于360°，
∴∠1+∠2=

1

2

×（360°-140°）=110°，
∴∠B′O′C′=180°-110°=70°；

（3）∵由（1）知，∠BOC=

180°+∠A

2

，
由（2）知，∠B′O′C′=180°-

180°+∠A

2

，
∴∠B′O′C′=180°-∠BOC．

点评：本题考查的是三角形内角和定理，熟知三角形内角和是180°是解答此题的关键．