题目内容
 如图,边长为a的正六边形内有两个三角形(数据如图),则
如图,边长为a的正六边形内有两个三角形(数据如图),则| S阴影 |
| S空白 |
考点:正多边形和圆,含30度角的直角三角形
专题:
分析:先求得两个三角形的面积,再求出正六边形的面积,求比值即可.
解答:
解:如图,
∵三角形的斜边长为a,
∴两条直角边长为
a,
a,
∴S空白=
a•
a=
a2,
∵AB=a,
∴OC=
a,
∴S正六边形=6×
a•
a=
a2,
∴S阴影=S正六边形-S空白=
a2-
a2=
a2,
∴
=
=5,
故答案为5.
∵三角形的斜边长为a,
∴两条直角边长为
| 1 |
| 2 |
| ||
| 2 |
∴S空白=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
∵AB=a,
∴OC=
| ||
| 2 |
∴S正六边形=6×
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 2 |
∴S阴影=S正六边形-S空白=
3
| ||
| 2 |
| ||
| 4 |
5
| ||
| 4 |
∴
| S阴影 |
| S空白 |
| ||||
|
故答案为5.
点评:本题考查了正多边形和圆,正六边形的边长等于半径,面积可以分成六个等边三角形的面积来计算.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
抛物线y=(x+2)2+3的顶点坐标是( )
| A、(-2,-3) |
| B、(2,3) |
| C、(-2,3) |
| D、(2,-3) |
 已知数a、b、c在数轴上的位置如图所示,则|a-c|-|a+b+c|-|b-a|=
已知数a、b、c在数轴上的位置如图所示,则|a-c|-|a+b+c|-|b-a|= 如图:⊙O1和⊙O2是等圆,外切于点A,过点A的直线交⊙O1于B点,交⊙O2于点C,求证:AB=AC.
如图:⊙O1和⊙O2是等圆,外切于点A,过点A的直线交⊙O1于B点,交⊙O2于点C,求证:AB=AC.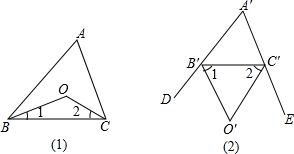
 如图,已知AB∥DE,AB=DE,AF=CD,∠CEF=90°.
如图,已知AB∥DE,AB=DE,AF=CD,∠CEF=90°. 某车间周内计划每天生产100辆电动车,由于工人实行轮休,每天上班人数不一定相等,实际每天生产量与计划量相比情况如下表(增加的车辆数为正数,减少的车辆数为负数)
某车间周内计划每天生产100辆电动车,由于工人实行轮休,每天上班人数不一定相等,实际每天生产量与计划量相比情况如下表(增加的车辆数为正数,减少的车辆数为负数)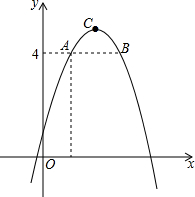 如图,二次函数y=ax2-4ax+b的图象过点A(1,4),B(x,4),该函数图象的顶点为C,且S△ABC=1,求二次函数的解析式.
如图,二次函数y=ax2-4ax+b的图象过点A(1,4),B(x,4),该函数图象的顶点为C,且S△ABC=1,求二次函数的解析式. 如图,AE⊥AB,BF⊥AB,AB的中垂线交AB于N,交EF于M,求证:MN=
如图,AE⊥AB,BF⊥AB,AB的中垂线交AB于N,交EF于M,求证:MN=