题目内容
 如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置OA,A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,按如图所示的直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=-x2+2x+
如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置OA,A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,按如图所示的直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=-x2+2x+| 7 |
| 4 |
考点:二次函数的应用
专题:
分析:如图,求水池的半径,实际是求OB的长.B点在抛物线上,且纵坐标为0,代入解析式解答即可.
解答:
 解:∵当x=0时,y=
解:∵当x=0时,y=
,
∴柱子OA的高度为
米;
在y=-x2+2x+
中,
当y=0时-x2+2x+
=0,
∴x1=
-1,x2=-1-
,
又∵x>0,
∴解得x=
-1米,
即水池的半径至少要
-1米才能使喷出的水流不至于落在池外.
 解:∵当x=0时,y=
解:∵当x=0时,y=| 7 |
| 4 |
∴柱子OA的高度为
| 7 |
| 4 |
在y=-x2+2x+
| 7 |
| 4 |
当y=0时-x2+2x+
| 7 |
| 4 |
∴x1=
| ||
| 2 |
| ||
| 2 |
又∵x>0,
∴解得x=
| ||
| 2 |
即水池的半径至少要
| ||
| 2 |
点评:本题考查了二次函数的实际应用,解题的关键是从实际问题中抽象出二次函数模型,难度中等.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
如图,把一些相同的菱形,按如图的方式排列,就构成一些大小不同的菱形,其中第一个图形中有3个菱形,第二个图形中有7个菱形,第三个图形中11个菱形,….则第n(n≥1)个图形中有菱形的个数为( )

| A、2n+3 | B、4n+3 |
| C、4n-1 | D、2n+2 |
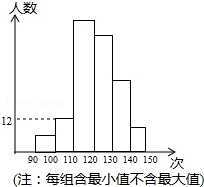 某民族学校对七年级学生进行跳绳测试,并抽取了部分学生的一分钟跳绳测试成绩进行整理,作出如图统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出第一组的频率为0.04,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:
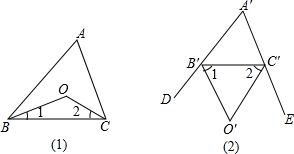
某民族学校对七年级学生进行跳绳测试,并抽取了部分学生的一分钟跳绳测试成绩进行整理,作出如图统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出第一组的频率为0.04,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题: 如图:⊙O1和⊙O2是等圆,外切于点A,过点A的直线交⊙O1于B点,交⊙O2于点C,求证:AB=AC.
如图:⊙O1和⊙O2是等圆,外切于点A,过点A的直线交⊙O1于B点,交⊙O2于点C,求证:AB=AC.