题目内容
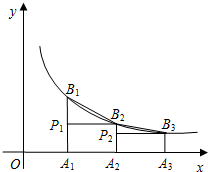 如图,已知A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…=An-1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y=
如图,已知A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…=An-1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y=| 1 |
| x |
(1)S1=
(2)S10=
(3)S1+S2+S3+…+Sn的和.
考点:反比例函数系数k的几何意义
专题:规律型
分析:由OA1=A1A2=A2A3=…=An-1An=1可知B1点的坐标为(1,y1),B2点的坐标为(2,y2),B3点的坐标为(3,y3)…Bn点的坐标为(n,yn),把x=1,x=2,x=3代入反比例函数的解析式即可求出y1、y2、y3的值,再由三角形的面积公式可得出S1、S2、S3…Sn的值,故可得出结论.
解答:解:(1)∵OA1=A1A2=A2A3=…=An-1An=1,
∴设B1(1,y1),B2(2,y2),B3(3,y3),…Bn(n,yn),
∵B1,B2,B3…Bn在反比例函数y=
(x>0)的图象上,
∴y1=1,y2=
,y3=
…yn=
,
∴S1=
×1×(y1-y2)=
×1×(1-
)=
(1-
);
∴S1=
;
(2)S10=
(
-
)=
;
(3)∵S1=
×1×(y1-y2)=
×1×(1-
)=
(1-
);
∴S2=
×1×(y2-y3)=
×(
-
);
S3=
×1×(y3-y4)=
×(
-
);
…
Sn=
(
-
),
∴S1+S2+S3+…+Sn=
(1-
+
-
+
-
+…+
-
)=
.
∵Sn=
(
-
),
故答案为:
,
.
∴设B1(1,y1),B2(2,y2),B3(3,y3),…Bn(n,yn),
∵B1,B2,B3…Bn在反比例函数y=
| 1 |
| x |
∴y1=1,y2=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
∴S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S1=
| 1 |
| 4 |
(2)S10=
| 1 |
| 2 |
| 1 |
| 10 |
| 1 |
| 11 |
| 1 |
| 220 |
(3)∵S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
S3=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
…
Sn=
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
∴S1+S2+S3+…+Sn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
| n |
| 2(n+1) |
∵Sn=
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
故答案为:
| 1 |
| 4 |
| 1 |
| 220 |
点评:本题考查的是反比例函数综合题,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
刘强在作业中的一道题:如图1,直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?刘强的做法是:如图2,画PC∥a,量出直线b与PC的夹角度数,即直线a,b所成角的度数.其依据是( )


| A、同位角相等,两直线平行 |
| B、同旁内角互补,两直线平行 |
| C、内错角相等,两直线平行 |
| D、两直线平行,同位角相等 |
如果两条平行线被第三条直线所截,那么其中一组同位角的角平分线( )
| A、垂直 | B、相交 |
| C、平行 | D、不能确定 |
在平面直角坐标系中,点P(5,-3)在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
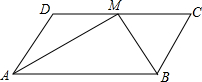 如图,在平行四边形ABCD中,M是CD的中点,AB=2BC,BM=a,AM=b,则CD的长为( )
如图,在平行四边形ABCD中,M是CD的中点,AB=2BC,BM=a,AM=b,则CD的长为( )A、
| ||
B、a+
| ||
C、
| ||
D、
|
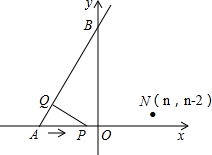 如图,已知射线AB与x轴和y轴分别交于点A(-3,0)和点B(0,3
如图,已知射线AB与x轴和y轴分别交于点A(-3,0)和点B(0,3