题目内容
如果两条平行线被第三条直线所截,那么其中一组同位角的角平分线( )
| A、垂直 | B、相交 |
| C、平行 | D、不能确定 |
考点:平行线的性质
专题:
分析:由两条平行线被第三条直线所截,根据两直线平行,同位角相等,即可得一组同位角相等即∠FEB=∠GFD,又由角平分线的性质求得∠1=∠2,然后根据同位角相等,两直线平行,即可求得答案.
解答: 解:∵AB∥CD,
解:∵AB∥CD,
∴∠FEB=∠GFD,
∵EM与FN分别是∠FEM与∠GFD的平分线,
∴∠1=
∠FEB,∠2=
∠GFD,
∴∠1=∠2,
∴EM∥FN.
故选C.
 解:∵AB∥CD,
解:∵AB∥CD,∴∠FEB=∠GFD,
∵EM与FN分别是∠FEM与∠GFD的平分线,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1=∠2,
∴EM∥FN.
故选C.
点评:本题考查了平行线性质的应用,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,题目比较好,难度适中.

练习册系列答案
相关题目
在下列四个图形中,△DEF能由△ABC经过平移得到的图形是( )
A、 |
B、 |
C、 |
D、 |
若方程组
的解互为相反数,则m的值是( )
|
| A、-7 | B、10 |
| C、-10 | D、-12 |
直线y=-x-2与y=x+4的交点在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若a-b=4,ab=2,则a2+b2的值为( )
| A、8 | B、12 | C、16 | D、20 |
已知点P(2-4m,m-2)在第二象限,则m的取值范围是( )
A、m>
| ||
| B、m<2 | ||
| C、m>2 | ||
D、
|
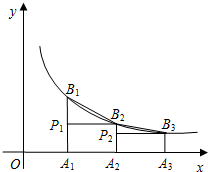 如图,已知A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…=An-1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y=
如图,已知A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…=An-1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y=