题目内容
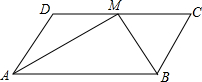 如图,在平行四边形ABCD中,M是CD的中点,AB=2BC,BM=a,AM=b,则CD的长为( )
如图,在平行四边形ABCD中,M是CD的中点,AB=2BC,BM=a,AM=b,则CD的长为( )A、
| ||
B、a+
| ||
C、
| ||
D、
|
考点:平行四边形的性质
专题:
分析:首先利用平行四边形的性质和已知条件证明△MAB为直角三角形,再利用勾股定理即可求出CD的长.
解答:解:∵M为CD中点,
∴CM=DM=
CD=
AB=BC=AD,
∴∠DAM=∠DMA,∠CBM=∠CMB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠C+∠D=180°,
∴∠C=2∠DMA,∠D=2∠CMB,
∴∠DMA+∠CMB=
(∠C+∠D)=90°,
∴∠AMB=180°-(∠DMA+∠CMB)=90°
即△MAB为直角三角形,
∵BM=a,AM=b,
∴CD=AB=
=
,
故选D.
∴CM=DM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DAM=∠DMA,∠CBM=∠CMB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠C+∠D=180°,
∴∠C=2∠DMA,∠D=2∠CMB,
∴∠DMA+∠CMB=
| 1 |
| 2 |
∴∠AMB=180°-(∠DMA+∠CMB)=90°
即△MAB为直角三角形,
∵BM=a,AM=b,
∴CD=AB=
| MA2+MB2 |
| a2+b2 |
故选D.
点评:本题考查了平行四边形的性质、等腰三角形的判定和性质以及直角三角形的判定和性质、勾股定理的运用,题目设计较好,综合性较强.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
在平面直角坐标系中,点P(5,-2014)在第( )象限.
| A、一 | B、二 | C、三 | D、四 |
直线y=-x-2与y=x+4的交点在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知点P(2-4m,m-2)在第二象限,则m的取值范围是( )
A、m>
| ||
| B、m<2 | ||
| C、m>2 | ||
D、
|
一个正方形的面积是10,估计它的边长大小在( )
| A、2和3之间 |
| B、3和4之间 |
| C、4和5之间 |
| D、5和6之间 |
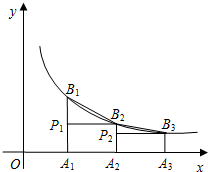 如图,已知A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…=An-1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y=
如图,已知A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…=An-1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y= 如图,在直角三角形中,两直角边长为a,b斜边上的高为h,判断以ab,ah,bh为边长的三角形形状并说明理由.
如图,在直角三角形中,两直角边长为a,b斜边上的高为h,判断以ab,ah,bh为边长的三角形形状并说明理由.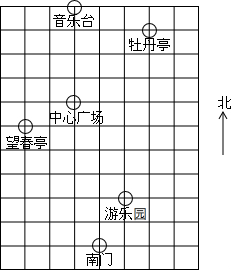 春天到了,七(2)班组织同学到公园春游,张明、李华对着景区示意图,如下描述牡丹园位置(图中小正方形边长代表100m)
春天到了,七(2)班组织同学到公园春游,张明、李华对着景区示意图,如下描述牡丹园位置(图中小正方形边长代表100m)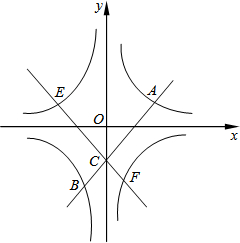 如图,在平面直角坐标系中,双曲线y=
如图,在平面直角坐标系中,双曲线y=