题目内容
2.解方程组:$\left\{\begin{array}{l}x-y=1\\ 4{x^2}-4xy+{y^2}=4\end{array}\right.$.分析 用代入法求解,由方程①得x=y+1,将该方程代入②,解该方程可得y的值,代回x=y+1可得x的值.
解答 解:解方程组$\left\{\begin{array}{l}{x-y=1}&{①}\\{4{x}^{2}-4xy+{y}^{2}=4}&{②}\end{array}\right.$,
由①得:x=y+1 ③,
把③代入②得:4(y+1)2-4y(y+1)+y2=4,
整理,得:y2+4y=0,
解得:y1=0,y2=-4,
把y=0代入③,得:x=1,
把y=-4代入③,得:x=-3.
故原方程组的解为:$\left\{\begin{array}{l}x=1\\ y=0\end{array}\right.$或$\left\{\begin{array}{l}x=-3\\ y=-4\end{array}\right.$;
点评 本题主要考查化归思想解高次方程的能力,用代入法把二元二次方程组转成一元二次方程来解是解题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
9.要登上某建筑物,靠墙有一架梯子,底端离建筑物3m,顶端离地面4m,则梯子的长度为( )
| A. | 2m | B. | 3m | C. | 4m | D. | 5m |
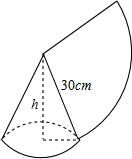 如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的高h等于20$\sqrt{2}$cm.
如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的高h等于20$\sqrt{2}$cm.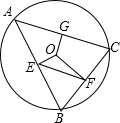 如图,⊙O的半径是$\sqrt{5}$,△ABC是⊙O的内接三角形,过圆心O分别作AB,BC,AC的垂线,垂足为E,F,G,连接EF,若OG=1,则EF的长为2.
如图,⊙O的半径是$\sqrt{5}$,△ABC是⊙O的内接三角形,过圆心O分别作AB,BC,AC的垂线,垂足为E,F,G,连接EF,若OG=1,则EF的长为2.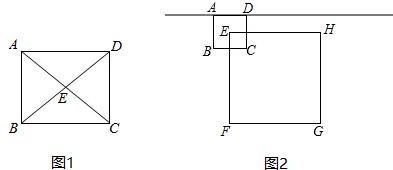
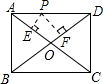 如图,P是矩形的边AD上一个动点,AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是2.4.
如图,P是矩形的边AD上一个动点,AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是2.4.