题目内容
15.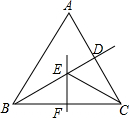 如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )
如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )| A. | 24° | B. | 30° | C. | 32° | D. | 36° |
分析 由EF是BC的垂直平分线,得到BE=CE,根据等腰三角形的性质得到∠EBC=∠ECB,由BD是∠ABC的平分线,得到∠ABD=∠CBD,根据三角形的内角和即可得到结论.
解答 解:∵EF是BC的垂直平分线,
∴BE=CE,
∴∠EBC=∠ECB,
∵BD是∠ABC的平分线,
∴∠ABD=∠CBD,
∴∠ABD=∠DBC=∠ECB,
∵∠BAC=60°,∠ACE=24°,
∴∠ABD=∠DBC=∠ECB=$\frac{1}{3}$(180°-60°-24°)=32°.
故选C.
点评 本题主要考查线段垂直平分线的性质,角平分线的定义,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键.

练习册系列答案
相关题目
5.在实数-2,6,0,1中,最小的实数是( )
| A. | -2 | B. | 6 | C. | 0 | D. | 1 |
19.在实数0.1,-5,0,-$\sqrt{3}$,π中,负数的个数是( )
| A. | 2 | B. | 1 | C. | 3 | D. | 4 |
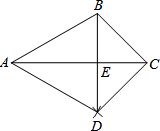 如图,已知△ABC,按如下步骤作图:
如图,已知△ABC,按如下步骤作图: 如图,在平行四边形ABCD中,AC、BD相交于O,请添加一个条件AC=BD或∠ABC=90°,可
如图,在平行四边形ABCD中,AC、BD相交于O,请添加一个条件AC=BD或∠ABC=90°,可