题目内容
17.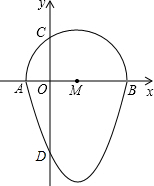 如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2-2x-3,求这个“果圆”被y轴截得线段CD的长3+$\sqrt{3}$.
如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2-2x-3,求这个“果圆”被y轴截得线段CD的长3+$\sqrt{3}$.
分析 将x=0代入抛物线的解析式得y=-3,故此可得到DO的长,然后令y=0可求得点A和点B的坐标,故此可得到AB的长,由M为圆心可得到MC和OM的长,然后依据勾股定理可求得OC的长,最后依据CD=OC+OD求解即可.
解答 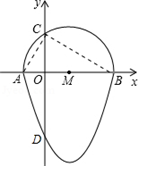 解:连接AC,BC.
解:连接AC,BC.
∵抛物线的解析式为y=x2-2x-3,
∴点D的坐标为(0,-3),
∴OD的长为3.
设y=0,则0=x2-2x-3,解得:x=-1或3,
∴A(-1,0),B(3,0).
∴AO=1,BO=3,AB=4,M(1,0).
∴MC=2,OM=1.
在Rt△COB中,OC=$\sqrt{C{M}^{2}-O{M}^{2}}$=$\sqrt{3}$.
∴CD=CO+OD=3+$\sqrt{3}$,即这个“果圆”被y轴截得的线段CD的长3+$\sqrt{3}$.
故答案为:3+$\sqrt{3}$.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了坐标轴上点的坐标特点,圆的概念和性质,勾股定理等知识点,求的点D的坐标以及OC的长是解题的关键.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
8. 如图是某几何体的三视图,这个几何体的侧面积是( )
如图是某几何体的三视图,这个几何体的侧面积是( )
 如图是某几何体的三视图,这个几何体的侧面积是( )
如图是某几何体的三视图,这个几何体的侧面积是( )| A. | 6π | B. | 2$\sqrt{10}$π | C. | $\sqrt{10}$π | D. | 3π |
6.下列运算正确的是( )
| A. | $\sqrt{12}$-$\sqrt{3}$=$\sqrt{3}$ | B. | (-3)2=6 | C. | 3a4-2a2=a2 | D. | (-a3)2=a5 |
7.“关于x的函数y=(1-m)x2+2x+1的图象与x轴至少有一个交点”是真命题,则m的值不可以是( )
| A. | m=1 | B. | m=0 | C. | m=-1 | D. | m=2 |
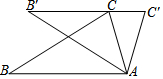 如图,把△ABC绕着点A顺时针方向旋转32°,得到△AB'C',恰好B',C,C'三点在一直线上,则么∠C'=74°.
如图,把△ABC绕着点A顺时针方向旋转32°,得到△AB'C',恰好B',C,C'三点在一直线上,则么∠C'=74°.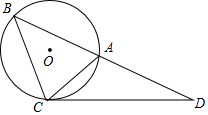 如图所示,△ABC的外接圆⊙O的半径为2,过点C作∠ACD=∠ABC,交BA的延长线于点D,若∠ABC=45°,∠D=30°.
如图所示,△ABC的外接圆⊙O的半径为2,过点C作∠ACD=∠ABC,交BA的延长线于点D,若∠ABC=45°,∠D=30°.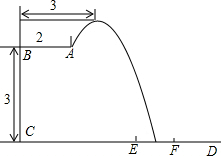 2016年里约奥运会,中国跳水队赢得8个项目中的7块金牌,优秀成绩的取得离不开艰辛的训练.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板AB长为2米,跳板距水面CD的高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米,现以CD为横轴,CB为纵轴建立直角坐标系.
2016年里约奥运会,中国跳水队赢得8个项目中的7块金牌,优秀成绩的取得离不开艰辛的训练.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板AB长为2米,跳板距水面CD的高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米,现以CD为横轴,CB为纵轴建立直角坐标系.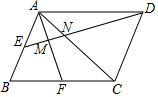 如图,点E,F分别是?ABCD两边AB、BC的中点,且AF、AC分别与ED交于M、N两点,有下列结论:①MN:ME=2:3;②MN:DN=1:4;③N是DE的三等分点;④△AMN~△DMA.其中正确的是:①③.(把所有正确结论的序号都选上)
如图,点E,F分别是?ABCD两边AB、BC的中点,且AF、AC分别与ED交于M、N两点,有下列结论:①MN:ME=2:3;②MN:DN=1:4;③N是DE的三等分点;④△AMN~△DMA.其中正确的是:①③.(把所有正确结论的序号都选上)