题目内容

7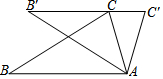．如图，把△ABC绕着点A顺时针方向旋转32°，得到△AB'C'，恰好B'，C，C'三点在一直线上，则么∠C'=74°．

分析 利用旋转的性质得出AC=AC′，以及∠CAC′的度数，再利用等腰三角形的性质得出答案．

解答 解：由题意可得：AC=AC′，
∵把△ABC绕着点A顺时针方向旋转34°，得到△AB′C′，点C刚好落在边B′C′上，
∴∠CAC′=32°，
∴∠ACC′=∠C′=$\frac{1}{2}$×（180°-32°）=74°．
故答案是：74°．

点评 此题主要考查了旋转的性质以及等腰三角形的性质等知识，根据题意得出AC=AC′是解题关键．

练习册系列答案
相关题目
17．已知在平面直角坐标系中，点A（a-3，-5）与点B（1，b+7）关于x轴对称，则$\sqrt{2a-3b}$的值为（精确到0.1）（　　）
A．3.4B．3.5C．3.6D．3.7
18．某地区修建一条长为6千米的公路．设每天的修建费为y（万元），修建天数为x天，当30≤x≤120时，y与x具有一次函数的关系，如表所示：
 x/万元 30 80120 
 y/万元 44n  26
（I）求y关于x（30≤x≤120）的函数解析式和n的值．
（Ⅱ）后来在修建的过程中计划发生改变，决定多修2千米，因此在没有增减建设力量的情况下，修完这条路比计划晚了15天，求原计划每天的修建费．
15．如图1，在⊙O中，弦AB与弦CD相交于点G，OA⊥CD于点E，延长CD，过点B作BF交CD的延长线于点F，使FB=FG．
（1）判断FB与⊙O的位置关系并证明你的结论；
（2）如图2，连接BD，AC，若BD=BG，求证：AC∥BF；
（3）在（2）的条件下，若tan∠F=$\frac{3}{4}$，GD=3，求⊙O的半径及BF的长．
2．如图，在平面直角坐标系中，点P从原点O出发．沿x轴向右以每秒一个单位长的速度运动t秒（t＞0），抛物线y=-x2+bx+c经过点O和点P．
（1）求c．b（用t的代数式表示）：
（2）抛物线y=-x2+bx+c与直线x=1和x=5分别交于M、N两点，当t＞1时，
①在点P的运动过程中，你认为sin∠MPO的大小是否会变化？若变化，说明理由；若不变，求出sin∠MPO的值：
②是否存在这样的/值，使得MP∥ON？如果存在，求出t值：如果不存在，请说明理由：
（3）横、纵坐标都是整数的点叫做整点，若抛物线在点O，P之间的部分与线段OP所围成的区域内（包括边界）恰有5个整点，结合函数的图象，直接写出t的取值范围．
12．已知一次函数y=kx+b，当x=2时，y=5；当x=-2时，y=-11，求k和b的值．
19．长方形的长是20，宽是x，周长是y，面积是S
（1）写出y和x之间的函数解析式；
（2）写出S与x之间函数解析式；
（3）指出自变量x的取值范围．
16．某商场要经营一种新上市的文具，进价为20元/件，试营销阶段发现：当销售单价25元/件时，每天的销售量是250件，销售单价每上涨1元，每天的销售量就减少10件．
（1）写出商场销售这种文具，每天所得的销售利润w（元）与销售单价x（元）之间的函数关系式；
（2）求销售单价为多少元时，该文具每天的销售利润最大；
（3）商场的营销部结合上述情况，提出了A、B两种营销方案：
方案A：该文具的销售单价高于进价且不超过30元；
方案B：每件文具的利润不低于25元且不高于29元．
请比较哪种方案的最大利润更高，并说明理由．
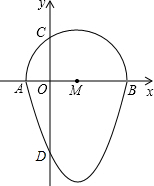17．如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”，已知点A、B、C、D分别是“果圆”与坐标轴的交点，AB为半圆的直径，抛物线的解析式为y=x2-2x-3，求这个“果圆”被y轴截得线段CD的长3+$\sqrt{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网