题目内容
7.“关于x的函数y=(1-m)x2+2x+1的图象与x轴至少有一个交点”是真命题,则m的值不可以是( )| A. | m=1 | B. | m=0 | C. | m=-1 | D. | m=2 |
分析 根据关于x的函数y=(1-m)x2+2x+1的图象与x轴至少有一个交点可分两种情况进行讨论,一种是此函数为一次函数,一种是此函数为二次函数,从而可以解答本题.
解答 解:∵关于x的函数y=(1-m)x2+2x+1的图象与x轴至少有一个交点,
∴当1-m=0,即m=1时,函数y=2x+1为一次函数,其解析式为y=2x+1,过一、二、三象限,与x轴只有一个交点;
当1-m≠0,即m≠1时,函数y=(1-m)x2+2x+1为二次函数,
△=22-4(1-m)≥0,
解得,m≥0.
由上可得,m的值为不小于零的数,
∴m的值不可能是-1,
故选C.
点评 本题考查了命题与定理、抛物线与x轴的交点、一次函数图象上点的坐标特征,解答本题的关键是明确题意,利用分类讨论的数学思想解答,难度不大,注意图象与x轴至少有一个交点.

练习册系列答案
相关题目
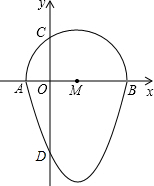 如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2-2x-3,求这个“果圆”被y轴截得线段CD的长3+$\sqrt{3}$.
如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2-2x-3,求这个“果圆”被y轴截得线段CD的长3+$\sqrt{3}$.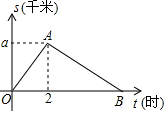 某单位举行“健康人生”徒步走活动,某人从起点体育村沿建设路到市生态园,再沿原路返回,设此人离开起点的路程s(千米)与走步时间t(小时)之间的函数关系如图所示,其中从起点到市生态园的平均速度是4千米/小时,用2小时,根据图象提供信息,解答下列问题.
某单位举行“健康人生”徒步走活动,某人从起点体育村沿建设路到市生态园,再沿原路返回,设此人离开起点的路程s(千米)与走步时间t(小时)之间的函数关系如图所示,其中从起点到市生态园的平均速度是4千米/小时,用2小时,根据图象提供信息,解答下列问题.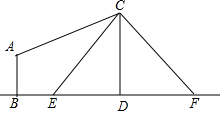 如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=$\sqrt{3}$米,BE=3米,求拉线CE的长.
如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=$\sqrt{3}$米,BE=3米,求拉线CE的长.
 如图,点A、B在直线l的两旁,在直线l上求作一点P,使|PA-PB|的值最大.(不写画法,请保留作图痕迹)
如图,点A、B在直线l的两旁,在直线l上求作一点P,使|PA-PB|的值最大.(不写画法,请保留作图痕迹)