题目内容
5.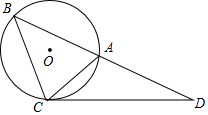 如图所示,△ABC的外接圆⊙O的半径为2,过点C作∠ACD=∠ABC,交BA的延长线于点D,若∠ABC=45°,∠D=30°.
如图所示,△ABC的外接圆⊙O的半径为2,过点C作∠ACD=∠ABC,交BA的延长线于点D,若∠ABC=45°,∠D=30°.(1)求证:CD是⊙O的切线;
(2)求$\widehat{AB}$的长.
分析 (1)证明:连接OA、OC,得到∠AOC=2∠ABC=90°,求得∠OCA=∠OAC=45°,于是得到OC⊥CD.由切线的判定定理即可得到结论;
(2)连接OB.根据三角形的内角和得到∠ACB=∠BCD-∠ACD=105°-45°=60°,由圆周角定理得到∠AOB=2∠ACB=120°,根据弧长公式即可得到结论.
解答 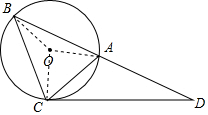 (1)证明:连接OA、OC.则∠AOC=2∠ABC=90°,
(1)证明:连接OA、OC.则∠AOC=2∠ABC=90°,
∵在△AOC中,OA=OC,
∴∠OCA=∠OAC=45°,
又∵∠ACD=45°,
∴∠OCD=∠OCA+∠ACD=45°+45°=90°,
∴OC⊥CD.
即CD是⊙O的切线;
(2)解:连接OB.
∵∠ABC=45°,∠D=30°,∠ACD=∠ABC=45°,
∴在△BCD中,∠BCD=180°-∠ABC-∠D=180°-45°-30°=105°,
∴∠ACB=∠BCD-∠ACD=105°-45°=60°,
∴∠AOB=2∠ACB=120°,
∴$\widehat{AB}$的长为:$\frac{120•π•2}{180}$=$\frac{4π}{3}$.
点评 本题考查了切线的判定,等腰三角形的性质,弧长的计算,正确的作出辅助线是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
20.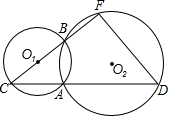 如图,已知⊙O1与⊙O2交于A,B两点,点C在⊙O1上且在⊙O2外,CA,CB的延长线分别与⊙O2交于点D,E,AC=3,AD=6,⊙O1的半径为2.则点O1到DE的距离为 ( )
如图,已知⊙O1与⊙O2交于A,B两点,点C在⊙O1上且在⊙O2外,CA,CB的延长线分别与⊙O2交于点D,E,AC=3,AD=6,⊙O1的半径为2.则点O1到DE的距离为 ( )
 如图,已知⊙O1与⊙O2交于A,B两点,点C在⊙O1上且在⊙O2外,CA,CB的延长线分别与⊙O2交于点D,E,AC=3,AD=6,⊙O1的半径为2.则点O1到DE的距离为 ( )
如图,已知⊙O1与⊙O2交于A,B两点,点C在⊙O1上且在⊙O2外,CA,CB的延长线分别与⊙O2交于点D,E,AC=3,AD=6,⊙O1的半径为2.则点O1到DE的距离为 ( )| A. | $\frac{17}{4}$ | B. | $\frac{9}{2}$ | C. | $\frac{19}{4}$ | D. | 5 |
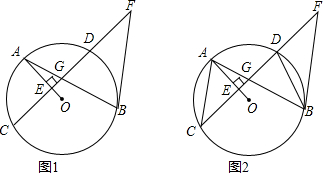
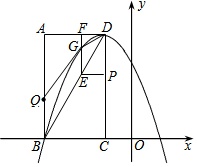 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点A(-3,4)、B(-3,0)、C(-1,0).以D为顶点的抛物线y=ax2+bx+c过点B.动点P从点D出发,沿DC边向点C运动,同时动点Q从点B出发,沿BA边向点A运动,点P、Q运动的速度均为每秒1个单位,运动的时间为t秒.过点P作PE⊥CD交BD于点E,过点E作EF⊥AD于点F,交抛物线于点G.
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点A(-3,4)、B(-3,0)、C(-1,0).以D为顶点的抛物线y=ax2+bx+c过点B.动点P从点D出发,沿DC边向点C运动,同时动点Q从点B出发,沿BA边向点A运动,点P、Q运动的速度均为每秒1个单位,运动的时间为t秒.过点P作PE⊥CD交BD于点E,过点E作EF⊥AD于点F,交抛物线于点G.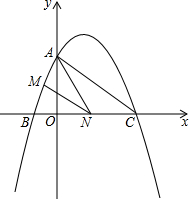 如图,已知二次函数y=ax2+$\frac{3}{2}$x+c的图象与y轴交于点A(0,4),与x轴交于点B,C,点C的坐标为(8,0),连接AC、AC.
如图,已知二次函数y=ax2+$\frac{3}{2}$x+c的图象与y轴交于点A(0,4),与x轴交于点B,C,点C的坐标为(8,0),连接AC、AC.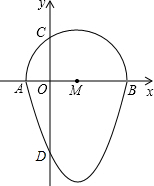 如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2-2x-3,求这个“果圆”被y轴截得线段CD的长3+$\sqrt{3}$.
如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2-2x-3,求这个“果圆”被y轴截得线段CD的长3+$\sqrt{3}$.