题目内容
8. 如图是某几何体的三视图,这个几何体的侧面积是( )
如图是某几何体的三视图,这个几何体的侧面积是( )| A. | 6π | B. | 2$\sqrt{10}$π | C. | $\sqrt{10}$π | D. | 3π |
分析 根据三视图可以判定此几何体为圆锥,根据三视图的尺寸可以知圆锥的底面半径为1,高为3,利用勾股定理求得圆锥的母线长为$\sqrt{10}$,代入公式求得即可.
解答 解:由三视图可知此几何体为圆锥,
∴圆锥的底面半径为1,高为3,
∴圆锥的母线长为$\sqrt{10}$,
∵圆锥的底面周长等于圆锥的侧面展开扇形的弧长,
∴圆锥的底面周长=圆锥的侧面展开扇形的弧长=2πr=2π×1=2π,
∴圆锥的侧面积=$\frac{1}{2}$lr=$\frac{1}{2}$×2π×$\sqrt{10}$=$\sqrt{10}$π,
故选C.
点评 本题考查了圆锥的侧面积的计算,解题的关键是正确的理解圆锥的底面周长等于圆锥的侧面展开扇形的面积.

练习册系列答案
相关题目
18.某地区修建一条长为6千米的公路.设每天的修建费为y(万元),修建天数为x天,当30≤x≤120时,y与x具有一次函数的关系,如表所示:
(I)求y关于x(30≤x≤120)的函数解析式和n的值.
(Ⅱ)后来在修建的过程中计划发生改变,决定多修2千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了15天,求原计划每天的修建费.
| x/万元 | 30 | 80 | 120 |
| y/万元 | 44 | n | 26 |
(Ⅱ)后来在修建的过程中计划发生改变,决定多修2千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了15天,求原计划每天的修建费.
20.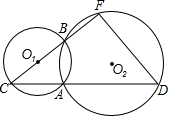 如图,已知⊙O1与⊙O2交于A,B两点,点C在⊙O1上且在⊙O2外,CA,CB的延长线分别与⊙O2交于点D,E,AC=3,AD=6,⊙O1的半径为2.则点O1到DE的距离为 ( )
如图,已知⊙O1与⊙O2交于A,B两点,点C在⊙O1上且在⊙O2外,CA,CB的延长线分别与⊙O2交于点D,E,AC=3,AD=6,⊙O1的半径为2.则点O1到DE的距离为 ( )
 如图,已知⊙O1与⊙O2交于A,B两点,点C在⊙O1上且在⊙O2外,CA,CB的延长线分别与⊙O2交于点D,E,AC=3,AD=6,⊙O1的半径为2.则点O1到DE的距离为 ( )
如图,已知⊙O1与⊙O2交于A,B两点,点C在⊙O1上且在⊙O2外,CA,CB的延长线分别与⊙O2交于点D,E,AC=3,AD=6,⊙O1的半径为2.则点O1到DE的距离为 ( )| A. | $\frac{17}{4}$ | B. | $\frac{9}{2}$ | C. | $\frac{19}{4}$ | D. | 5 |
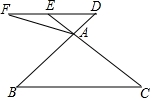 如图,在△ABC中,点D是BA边延长线上一点,过点D作DE∥BC,交CA延长线于点E,点F是DE延长线上一点,连接AF.
如图,在△ABC中,点D是BA边延长线上一点,过点D作DE∥BC,交CA延长线于点E,点F是DE延长线上一点,连接AF.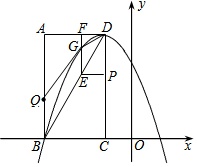 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点A(-3,4)、B(-3,0)、C(-1,0).以D为顶点的抛物线y=ax2+bx+c过点B.动点P从点D出发,沿DC边向点C运动,同时动点Q从点B出发,沿BA边向点A运动,点P、Q运动的速度均为每秒1个单位,运动的时间为t秒.过点P作PE⊥CD交BD于点E,过点E作EF⊥AD于点F,交抛物线于点G.
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点A(-3,4)、B(-3,0)、C(-1,0).以D为顶点的抛物线y=ax2+bx+c过点B.动点P从点D出发,沿DC边向点C运动,同时动点Q从点B出发,沿BA边向点A运动,点P、Q运动的速度均为每秒1个单位,运动的时间为t秒.过点P作PE⊥CD交BD于点E,过点E作EF⊥AD于点F,交抛物线于点G.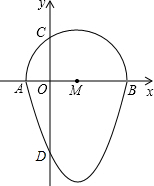 如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2-2x-3,求这个“果圆”被y轴截得线段CD的长3+$\sqrt{3}$.
如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2-2x-3,求这个“果圆”被y轴截得线段CD的长3+$\sqrt{3}$.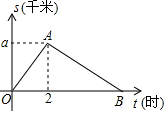 某单位举行“健康人生”徒步走活动,某人从起点体育村沿建设路到市生态园,再沿原路返回,设此人离开起点的路程s(千米)与走步时间t(小时)之间的函数关系如图所示,其中从起点到市生态园的平均速度是4千米/小时,用2小时,根据图象提供信息,解答下列问题.
某单位举行“健康人生”徒步走活动,某人从起点体育村沿建设路到市生态园,再沿原路返回,设此人离开起点的路程s(千米)与走步时间t(小时)之间的函数关系如图所示,其中从起点到市生态园的平均速度是4千米/小时,用2小时,根据图象提供信息,解答下列问题.