题目内容
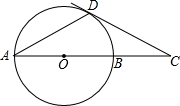 如图,⊙O的直径AB=6cm,D为⊙O上一点,∠BAD=30°,过点D的切线交AB的延长线于点C.则∠ADC的度数是
如图,⊙O的直径AB=6cm,D为⊙O上一点,∠BAD=30°,过点D的切线交AB的延长线于点C.则∠ADC的度数是考点:切线的性质
专题:
分析:连接OD,那么OD⊥CD,这时∠ADC=∠ADO+90°,我们不难发现∠ADO=∠A=30°,因此∠DC=120°;根据三角形的内角和,那么∠C=30°,直角三角形ODC中,有OD的长,∠C=30°,可求出OC的值,也就求出了AC的长.
解答: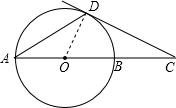 解:连接OD,
解:连接OD,
∵AO=OD,
∴∠ADO=∠DAO=30°,
∵CD是⊙O的切线,
∴∠CDO=90°,
∴∠ADC=∠ADO+∠CDO=30°+90°=120°;
∵∠ADO=∠DAO=30°,
∴∠COD=60°,
∵OD=AO=
AB=3cm,
在Rt△COD中,∠C=30°,
∴OC=2OD=6cm,
∴AC=AO+OC=3+6=9cm.
故答案为:120,9cm.
 解:连接OD,
解:连接OD,∵AO=OD,
∴∠ADO=∠DAO=30°,
∵CD是⊙O的切线,
∴∠CDO=90°,
∴∠ADC=∠ADO+∠CDO=30°+90°=120°;
∵∠ADO=∠DAO=30°,
∴∠COD=60°,
∵OD=AO=
| 1 |
| 2 |
在Rt△COD中,∠C=30°,
∴OC=2OD=6cm,
∴AC=AO+OC=3+6=9cm.
故答案为:120,9cm.
点评:本题考查了切线的性质和解直角三角形,根据切线的性质准确的作出辅助线,构建直角三角形是解题的关键.

练习册系列答案
相关题目
用配方法解方程x2+6x+7=0,则方程可变为( )
| A、(x-3)2=2 |
| B、(x+3)2=2 |
| C、(x-6)2=12 |
| D、(x+6)2=49 |
 已知:如图,在△ABC中,∠ABC,∠ACB的平分线相交于点P,
已知:如图,在△ABC中,∠ABC,∠ACB的平分线相交于点P,
 如图,△ADE∽△ACB,则DE:BC=
如图,△ADE∽△ACB,则DE:BC= 如图,在⊙O中,
如图,在⊙O中,
 如图所示,直线BC经过原点O,点A在x轴上,AD⊥BC于D,若B(m,2),C(n,-3),A(2,0),则AD•BC=
如图所示,直线BC经过原点O,点A在x轴上,AD⊥BC于D,若B(m,2),C(n,-3),A(2,0),则AD•BC=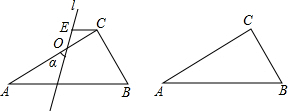 如图,在△ABC中,∠ACB=90°,∠B=60°.O是AC的中点,过点A、C的直线L绕点O按逆时针方向旋α角,交边AB于点D,作CE∥AB交直线L于点E.当∠α=90°时,判断四边形EDBC是否菱形,并说明理由.
如图,在△ABC中,∠ACB=90°,∠B=60°.O是AC的中点,过点A、C的直线L绕点O按逆时针方向旋α角,交边AB于点D,作CE∥AB交直线L于点E.当∠α=90°时,判断四边形EDBC是否菱形,并说明理由.