题目内容

用配方法解方程x2+6x+7=0，则方程可变为（　　）
A、（x-3）2=2
B、（x+3）2=2
C、（x-6）2=12
D、（x+6）2=49
考点：解一元二次方程-配方法
专题：计算题
分析：方程移项后，配方得到结果，即可做出判断．
解答：解：方程移项得：x2+6x=-7，
配方得：x2+6x+9=2，即（x+3）2=2，
故选：B．
点评：此题考查了解一元二次方程-配方法，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
相关题目
设n为整数，下列式子中表示偶数的是（　　）
A、2nB、2n+1
C、2n-1D、n+2
如图，在Rt△ABC中：
（1）若AC=5，BC=12，求AB的长；
（2）若AB=25，AC=20，求BC的长．
已知一元二次方程x2+3x-1=0，下列判断正确的是（　　）
A、该方程有两个相等的实数根
B、该方程有两个不相等的实数根
C、该方程无实数根
D、该方程根的情况不确定
已知3是关于x的方程5x-a=3的解，则a的值是（　　）
A、-14B、12
C、14D、-13
若方程x|m|-2-1=0是一个一元一次方程，则m等于（　　）
A、-3B、3C、±3D、±2
把方程
x-1
0.2
-
0.5x+1
0.3
=1中的分数转化为整数，结果（　　）
A、
10x-1
2
-
5x+1
3
=1
B、
10x-1
2
-
5x+1
3
=10
C、
10x-10
2
-
5x+10
3
=10
D、
10x-10
2
-
5x+10
3
=1
计算：
（1）3c3-2c2+8c-13c3+2c-2c2+3               
（2）8x2-4（2x2+3x-1）
（3）5x2-2（3y2-5x2）+（-4y2+7xy）．
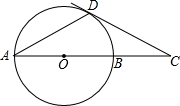如图，⊙O的直径AB=6cm，D为⊙O上一点，∠BAD=30°，过点D的切线交AB的延长线于点C．则∠ADC的度数是
 
； AC的长是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网