题目内容
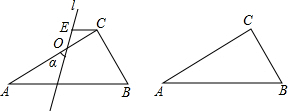 如图,在△ABC中,∠ACB=90°,∠B=60°.O是AC的中点,过点A、C的直线L绕点O按逆时针方向旋α角,交边AB于点D,作CE∥AB交直线L于点E.当∠α=90°时,判断四边形EDBC是否菱形,并说明理由.
如图,在△ABC中,∠ACB=90°,∠B=60°.O是AC的中点,过点A、C的直线L绕点O按逆时针方向旋α角,交边AB于点D,作CE∥AB交直线L于点E.当∠α=90°时,判断四边形EDBC是否菱形,并说明理由.考点:菱形的判定,旋转的性质
专题:
分析:根据∠α=∠ACB=90°先证明四边形EDBC是平行四边形.再利用Rt△ABC中,∠ACB=90°,∠B=60°,BC=2求得AB,AC,AO的长度;在Rt△AOD中,∠A=30°,AD=2,可求BD,比较得BD=BC,可证明四边形EDBC是菱形.
解答:解:当∠α=90°时,四边形EDBC是菱形.
∵∠α=∠ACB=90°,
∴BC∥ED,
∵CE∥AB,
∴四边形EDBC是平行四边形.
在Rt△ABC中,∠ACB=90°,∠B=60°,设BC=2t,
∴∠A=30°,
∴AB=4t,AC=2
t,
∴AO=
AC=
t.
在Rt△AOD中,∠A=30°,OD=
AD,
AD=
=
,
∴AD=2t,
∴BD=2t,
∴BD=BC.
又∵四边形EDBC是平行四边形,
∴四边形EDBC是菱形.

∵∠α=∠ACB=90°,
∴BC∥ED,
∵CE∥AB,
∴四边形EDBC是平行四边形.
在Rt△ABC中,∠ACB=90°,∠B=60°,设BC=2t,
∴∠A=30°,
∴AB=4t,AC=2
| 3 |
∴AO=
| 1 |
| 2 |
| 3 |
在Rt△AOD中,∠A=30°,OD=
| 1 |
| 2 |
AD=
| OA2+OD2 |
(
|
∴AD=2t,
∴BD=2t,
∴BD=BC.
又∵四边形EDBC是平行四边形,
∴四边形EDBC是菱形.
点评:此题考查了菱形的判定勾股定理以及含30°角的直角三角形的性质.此题难度较大,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
相关题目
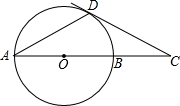 如图,⊙O的直径AB=6cm,D为⊙O上一点,∠BAD=30°,过点D的切线交AB的延长线于点C.则∠ADC的度数是
如图,⊙O的直径AB=6cm,D为⊙O上一点,∠BAD=30°,过点D的切线交AB的延长线于点C.则∠ADC的度数是 甲、乙两人用如图所示的两个分格均匀的转盘做游戏:分别转动两个转盘,若转盘停止后,指针指向一个数字(若指针恰好停在分格线上,则重转一次),用所指的两个数字作乘积,如果积大于10,那么甲获胜;如果积不大于10,那么乙获胜.清你解决下列问题:
甲、乙两人用如图所示的两个分格均匀的转盘做游戏:分别转动两个转盘,若转盘停止后,指针指向一个数字(若指针恰好停在分格线上,则重转一次),用所指的两个数字作乘积,如果积大于10,那么甲获胜;如果积不大于10,那么乙获胜.清你解决下列问题: 如图已知△ABC,
如图已知△ABC, 如图,已知:∠BME=∠CPF,直线EF分别交AB、CD于M、P,MN、PQ分别平分∠AME、∠DPF,求证:
如图,已知:∠BME=∠CPF,直线EF分别交AB、CD于M、P,MN、PQ分别平分∠AME、∠DPF,求证: 如图,已知CF⊥AB于点E,且AE=EB,∠B=40°.求∠ACD、∠DCF的度数.
如图,已知CF⊥AB于点E,且AE=EB,∠B=40°.求∠ACD、∠DCF的度数.
 如图,已知AB=DC,∠ABC=∠DCB.求证:△ABC≌△DCB.
如图,已知AB=DC,∠ABC=∠DCB.求证:△ABC≌△DCB. 如图,AB∥CD,∠BAE=30°,∠ECD=60°,求∠AEC的度数.
如图,AB∥CD,∠BAE=30°,∠ECD=60°,求∠AEC的度数.