题目内容
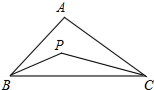 已知:如图,在△ABC中,∠ABC,∠ACB的平分线相交于点P,
已知:如图,在△ABC中,∠ABC,∠ACB的平分线相交于点P,(1)若∠A=80°,求∠BPC的度数;
(2)设∠A=n°(n为已知数),求∠BPC的度数;
(3)当∠A为多少度时,∠BPC=3∠A?
考点:三角形内角和定理,三角形的外角性质
专题:计算题
分析:(1)根据角平分线的定义得到∠1=
∠ABC,∠2=
∠ACB,再利用三角形内角和定理得∠BPC=180°-∠1-∠2,∠ABC+∠ACB=180°-∠A,则∠BPC=180°-
(180°-∠A),整理得到∠BPC=90°+
∠A,然后把∠A=80°代入计算即可;
(2)把∠A=n°代入(1)中的结论即可;
(3)由(1)的结论得∠BPC=90°+
∠A,加上∠BPC=3∠A,则3∠A=90°+
∠A,然后解方程即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)把∠A=n°代入(1)中的结论即可;
(3)由(1)的结论得∠BPC=90°+
| 1 |
| 2 |
| 1 |
| 2 |
解答:解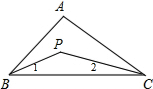 :(1)∵∠ABC,∠ACB的平分线相交于点P,
:(1)∵∠ABC,∠ACB的平分线相交于点P,
∴∠1=
∠ABC,∠2=
∠ACB,
∵∠BPC=180°-∠1-∠2,
∴∠BPC=180°-
(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°-∠A,
∴∠BPC=180°-
(180°-∠A)
=90°+
∠A
当∠A=80°时,∠BPC=90°+
×80°=130°;
(2)当∠A=n°时,∠BPC=90°+
n°;
(3)∵∠BPC=90°+
∠A,
而∠BPC=3∠A,
∴3∠A=90°+
∠A,
∴∠A=36°.
 :(1)∵∠ABC,∠ACB的平分线相交于点P,
:(1)∵∠ABC,∠ACB的平分线相交于点P,∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BPC=180°-∠1-∠2,
∴∠BPC=180°-
| 1 |
| 2 |
∵∠ABC+∠ACB=180°-∠A,
∴∠BPC=180°-
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
当∠A=80°时,∠BPC=90°+
| 1 |
| 2 |
(2)当∠A=n°时,∠BPC=90°+
| 1 |
| 2 |
(3)∵∠BPC=90°+
| 1 |
| 2 |
而∠BPC=3∠A,
∴3∠A=90°+
| 1 |
| 2 |
∴∠A=36°.
点评:本题考查了三角形内角和定理:三角形内角和是180°.也考查了角平分线定义和角的计算;关键得出∠BPC与∠A的数量关系.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
已知一元二次方程x2+3x-1=0,下列判断正确的是( )
| A、该方程有两个相等的实数根 |
| B、该方程有两个不相等的实数根 |
| C、该方程无实数根 |
| D、该方程根的情况不确定 |
 如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.
如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.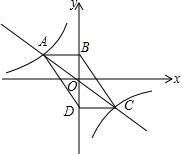 如图,A、C是双曲线上关于原点O对称的任意两点,AB垂直y轴于B,CD垂直y轴于D,且四边形ABCD的面积为6,则这个函数的解析式为
如图,A、C是双曲线上关于原点O对称的任意两点,AB垂直y轴于B,CD垂直y轴于D,且四边形ABCD的面积为6,则这个函数的解析式为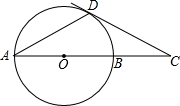 如图,⊙O的直径AB=6cm,D为⊙O上一点,∠BAD=30°,过点D的切线交AB的延长线于点C.则∠ADC的度数是
如图,⊙O的直径AB=6cm,D为⊙O上一点,∠BAD=30°,过点D的切线交AB的延长线于点C.则∠ADC的度数是 如图是某地气温t(℃)随着高度h(千米)的增加而降低的关系图,观察图象可知该地地面气温是
如图是某地气温t(℃)随着高度h(千米)的增加而降低的关系图,观察图象可知该地地面气温是 如图已知△ABC,
如图已知△ABC,