题目内容
12.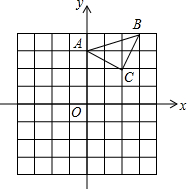 已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)(1)画出△ABC向下平移4个单位,再向左平移1个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)作出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2,并直接写出C2点的坐标;
(3)作出△ABC关于原点O成中心对称的△A3B3C3,并直接写出B3的坐标.
分析 (1)将A、B、C分别向下平移4个单位,再向左平移1个单位,顺次连接即可得出△A1B1C1,即可得出写出C1点的坐标;
(2)根据旋转的性质,找到各点的对应点,顺次连接可得出△A2B2C2,即可写出C2点的坐标;
(3)根据关于原点对称的性质,找到各点的对应点,顺次连接可得出△A3B3C3,即可写出C3点的坐标.
解答 解:(1)如图1,C1(1,-2)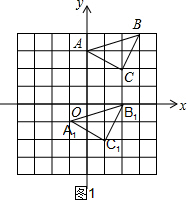
(2)如图2,C2(-1,1)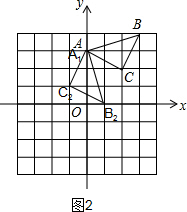
(3)如图3,B3(-3,-4)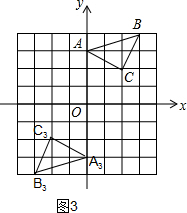
点评 本题考查了旋转作图及平移作图的知识,解答此类题目的关键是就是寻找对应点,要求掌握旋转三要素、平移的特点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.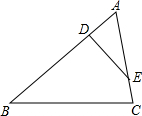 如图,D,E分别是△ABC的边AB,AC上的点,$\frac{BD}{AD}$=$\frac{AE}{CE}$=3,且∠AED=∠B,则△AED与△ABC的面积比是( )
如图,D,E分别是△ABC的边AB,AC上的点,$\frac{BD}{AD}$=$\frac{AE}{CE}$=3,且∠AED=∠B,则△AED与△ABC的面积比是( )
 如图,D,E分别是△ABC的边AB,AC上的点,$\frac{BD}{AD}$=$\frac{AE}{CE}$=3,且∠AED=∠B,则△AED与△ABC的面积比是( )
如图,D,E分别是△ABC的边AB,AC上的点,$\frac{BD}{AD}$=$\frac{AE}{CE}$=3,且∠AED=∠B,则△AED与△ABC的面积比是( )| A. | 1:2 | B. | 1:3 | C. | 3:16 | D. | 4:9 |
7.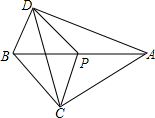 如图,点P在线段AB上,PA=PB=PC=PD,当∠BPC=60°时,∠BDC=( )
如图,点P在线段AB上,PA=PB=PC=PD,当∠BPC=60°时,∠BDC=( )
 如图,点P在线段AB上,PA=PB=PC=PD,当∠BPC=60°时,∠BDC=( )
如图,点P在线段AB上,PA=PB=PC=PD,当∠BPC=60°时,∠BDC=( )| A. | 15° | B. | 30° | C. | 25° | D. | 60° |
 如图所示的图形是由5个完全相同的小正方体组成的立体图形,则这个几何体的俯视图是( )
如图所示的图形是由5个完全相同的小正方体组成的立体图形,则这个几何体的俯视图是( )



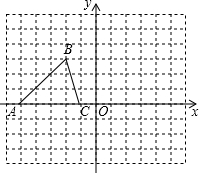 已知△ABC的三个顶点的坐标分别为A(-5,0)、B(-2,3)、C(-1,0)将△ABC绕坐标原点顺时针旋转90°,画出对应的△A′B′C′图形,
已知△ABC的三个顶点的坐标分别为A(-5,0)、B(-2,3)、C(-1,0)将△ABC绕坐标原点顺时针旋转90°,画出对应的△A′B′C′图形,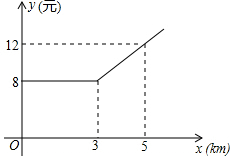 某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,若某乘客有一次乘出租车的车费为42元,则这位乘客乘车的里程为20km.
某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,若某乘客有一次乘出租车的车费为42元,则这位乘客乘车的里程为20km. 如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1
如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1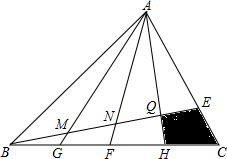 如图,设△ABC的面积为10cm2,若CE=$\frac{1}{4}$AC,BG=GF=FH=HC,求阴影四边形的面积.
如图,设△ABC的面积为10cm2,若CE=$\frac{1}{4}$AC,BG=GF=FH=HC,求阴影四边形的面积.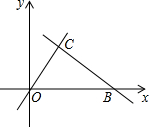 如图,直线OC、BC的函数关系式为y=x与y=-2x+6,点P(t,0)是线段OB上一动点,过P作直线l与x轴垂直.
如图,直线OC、BC的函数关系式为y=x与y=-2x+6,点P(t,0)是线段OB上一动点,过P作直线l与x轴垂直.