题目内容
20.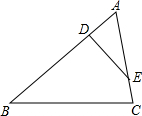 如图,D,E分别是△ABC的边AB,AC上的点,$\frac{BD}{AD}$=$\frac{AE}{CE}$=3,且∠AED=∠B,则△AED与△ABC的面积比是( )
如图,D,E分别是△ABC的边AB,AC上的点,$\frac{BD}{AD}$=$\frac{AE}{CE}$=3,且∠AED=∠B,则△AED与△ABC的面积比是( )| A. | 1:2 | B. | 1:3 | C. | 3:16 | D. | 4:9 |
分析 根据∠AED=∠B,∠A=∠A,证得△ADE∽△ACB,得到比例式$\frac{AD}{AC}=\frac{AE}{AB}$,又$\frac{BD}{AD}$=$\frac{AE}{CE}$=3,得到AD=$\frac{1}{4}$AB,AE=$\frac{3}{4}$AC,于是推出4AD2=$\frac{3}{4}$AC2得到$\frac{A{D}^{2}}{A{C}^{2}}$=$\frac{3}{16}$,然后根据相似三角形的性质即可得到结论.
解答 解:∵∠AED=∠B,∠A=∠A,
∴△ADE∽△ACB,
∴$\frac{AD}{AC}=\frac{AE}{AB}$,
∵$\frac{BD}{AD}$=$\frac{AE}{CE}$=3,
∴AD=$\frac{1}{4}$AB,AE=$\frac{3}{4}$AC,
∴4AD2=$\frac{3}{4}$AC2
∴$\frac{A{D}^{2}}{A{C}^{2}}$=$\frac{3}{16}$,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{A{D}^{2}}{A{C}^{2}}$=$\frac{3}{16}$,
故选C.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质定理是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
8.在平面中,下列说法正确的是( )
| A. | 四边相等的四边形是正方形 | |
| B. | 四个角相等的四边形是矩形 | |
| C. | 对角线相等的四边形是菱形 | |
| D. | 对角线互相垂直的四边形是平行四边形 |
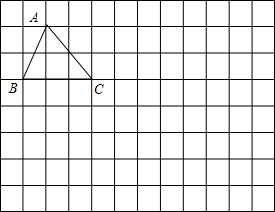 将如图所示的三角形ABC,先水平向右平移5格得三角形DEF,再竖直向下平移4格得到三角形GHQ,作出这两个三角形,并标上字母.
将如图所示的三角形ABC,先水平向右平移5格得三角形DEF,再竖直向下平移4格得到三角形GHQ,作出这两个三角形,并标上字母.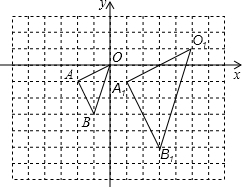 在如图的方格中,△OAB的顶点坐标分别为O(0,0)、A(-2,-1)、B(-1,-3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.
在如图的方格中,△OAB的顶点坐标分别为O(0,0)、A(-2,-1)、B(-1,-3),△O1A1B1与△OAB是关于点P为位似中心的位似图形. 已知等腰Rt△ABC与等腰Rt△DBE,F为AE中点,G为CD中点,连结GF.判断FG与DC的位置关系和数量关系.
已知等腰Rt△ABC与等腰Rt△DBE,F为AE中点,G为CD中点,连结GF.判断FG与DC的位置关系和数量关系.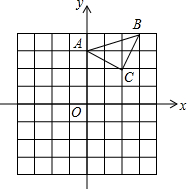 已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)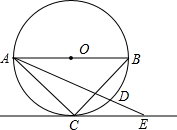 已知AB为⊙O的直径,$\widehat{BD}$=2$\widehat{CD}$,CE∥AB切⊙O于C点,交AD延长线于E点,若⊙O半径为2cm,求AE的长.
已知AB为⊙O的直径,$\widehat{BD}$=2$\widehat{CD}$,CE∥AB切⊙O于C点,交AD延长线于E点,若⊙O半径为2cm,求AE的长.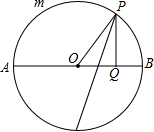 如图,有一定圆O,直径为AB,今有一动点P在半圆AmB上移动,过点P作AB的垂线PQ,试证:∠OPQ的平分线恒通过一定点.
如图,有一定圆O,直径为AB,今有一动点P在半圆AmB上移动,过点P作AB的垂线PQ,试证:∠OPQ的平分线恒通过一定点.