题目内容
17.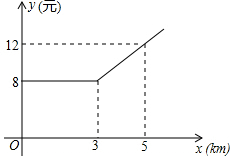 某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,若某乘客有一次乘出租车的车费为42元,则这位乘客乘车的里程为20km.
某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,若某乘客有一次乘出租车的车费为42元,则这位乘客乘车的里程为20km.
分析 根据函数图象可以得出出租车的起步价是8元,设当x>3时,y与x的函数关系式为y=kx+b,运用待定系数法求出一次函数解析式,将y=42代入解析式就可以求出x的值.
解答 解:由图象得:出租车的起步价是8元;
设当x>3时,y与x的函数关系式为y=kx+b(k≠0),由函数图象,得
$\left\{\begin{array}{l}{8=3k+b}\\{12=5k+b}\end{array}\right.$,
解得:
$\left\{\begin{array}{l}{k=2}\\{b=2}\end{array}\right.$,
故y与x的函数关系式为:y=2x+2;
∵42元>8元,
∴当y=42时,
42=2x+2,
x=20
答:这位乘客乘车的里程是20km.
点评 本题考查了待定系数法求一次函数的解析式的运用,解答时理解函数图象是重点,求出函数的解析式是关键.

练习册系列答案
相关题目
7.点A(-3,-2)向上平移2个单位,再向左平移2个单位到点B,则点B的坐标为( )
| A. | (1,0) | B. | (-1,-4) | C. | (-1,0) | D. | (-5,0) |
8.在平面中,下列说法正确的是( )
| A. | 四边相等的四边形是正方形 | |
| B. | 四个角相等的四边形是矩形 | |
| C. | 对角线相等的四边形是菱形 | |
| D. | 对角线互相垂直的四边形是平行四边形 |
6.一个直角三角形两直角边的比为3:2,斜边上的高分得的两个直角三角形的面积分别为S1和S2(S1<S2),则S1:S2=( )
| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{2}$ |
 已知等腰Rt△ABC与等腰Rt△DBE,F为AE中点,G为CD中点,连结GF.判断FG与DC的位置关系和数量关系.
已知等腰Rt△ABC与等腰Rt△DBE,F为AE中点,G为CD中点,连结GF.判断FG与DC的位置关系和数量关系.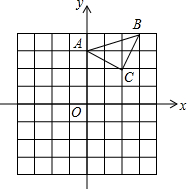 已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)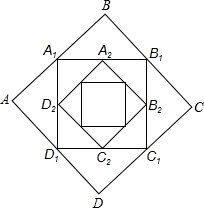 如图,正方形ABCD的边长为2,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,顺次连接正方形A1B1C1D1 四边的中点得到第二个正方形A2B2C2D2…以此类推,则第n个正方形AnBnCnDn的面积是($\frac{1}{2}$)n-2.
如图,正方形ABCD的边长为2,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,顺次连接正方形A1B1C1D1 四边的中点得到第二个正方形A2B2C2D2…以此类推,则第n个正方形AnBnCnDn的面积是($\frac{1}{2}$)n-2.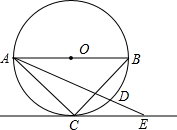 已知AB为⊙O的直径,$\widehat{BD}$=2$\widehat{CD}$,CE∥AB切⊙O于C点,交AD延长线于E点,若⊙O半径为2cm,求AE的长.
已知AB为⊙O的直径,$\widehat{BD}$=2$\widehat{CD}$,CE∥AB切⊙O于C点,交AD延长线于E点,若⊙O半径为2cm,求AE的长.