题目内容
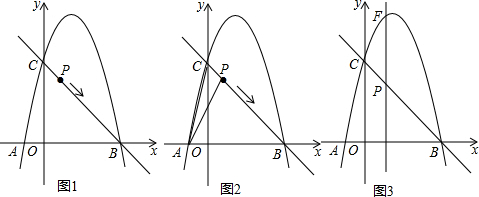
10.如图1,抛物线y=ax2+bx+4的图象过A(-1,0),B(4,0)两点,与y轴交于点C,作直线BC,动点P从点C出发,以每秒$\sqrt{2}$个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.(1)求抛物线的表达式;
(2)如图2,当t=1时,求S△ACP的面积;
(3)如图3,过点P向x轴作垂线分别交x轴,抛物线于E、F两点.
①求PF的长度关于t的函数表达式,并求出PF的长度的最大值;
②连接CF,将△PCF沿CF折叠得到△P′CF,当t为何值时,四边形PFP′C是菱形?
分析 (1)将A、B点的坐标代入函数解析式中,即可得到关于a、b的二元一次方程,解方程即可得出结论;
(2)令x=0可得出C点的坐标,设出直线BC解析式y=kx+4,代入B点坐标可求出k值,利用面积法求出点A到直线BC的距离结合三角形的面积,即可得出结论;
(3)①由直线BC的解析式为y=-x+4可得知OE=$\frac{\sqrt{2}}{2}$CP,设出P、F点的坐标,由F点的纵坐标-P点的纵坐标即可得出PF的长度关于t的函数表达式,结合二次函数的性质即可求出最值问题;②由翻转特性可知PC=P′C,PF=P′F,若四边形PFP′C是菱形,则有PC=PF,由此得出关于t的二元一次方程,解方程即可得出结论.
解答 解:(1)∵抛物线y=ax2+bx+4的图象过A(-1,0),B(4,0)两点,
∴$\left\{\begin{array}{l}{a-b+4=0}\\{16a+4b+4=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-1}\\{b=3}\end{array}\right.$.
∴抛物线的表达式为y=-x2+3x+4.
(2)令x=0,则y=4,
即点C的坐标为(0,4),
∴BC=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$.
设直线BC的解析式为y=kx+4,
∵点B的坐标为(4,0),
∴0=4k+4,解得k=-1,
∴直线BC的解析式为y=-x+4.
当t=1时,CP=$\sqrt{2}$,
点A(-1,0)到直线BC的距离h=$\frac{AB•OC}{BC}$=$\frac{[4-(-1)]×4}{4\sqrt{2}}$=$\frac{5\sqrt{2}}{2}$,
S△ACP=$\frac{1}{2}$CP•h=$\frac{1}{2}$×$\sqrt{2}$×$\frac{5\sqrt{2}}{2}$=$\frac{5}{2}$.
(3)①∵直线BC的解析式为y=-x+4,
∴CP=$\sqrt{2}$t,OE=t,设P(t,-t+4),F(t,-t2+3t+4),(0≤t≤4)
PF=-t2+3t+4-(-t+4)=-t2+4t,(0≤t≤4).
当t=-$\frac{4}{2×(-1)}$=2时,PF取最大值,最大值为4.
②∵△PCF沿CF折叠得到△P′CF,
∴PC=P′C,PF=P′F,
当四边形PFP′C是菱形时,只需PC=PF.
∴$\sqrt{2}$t=-t2+4t,
解得:t1=0(舍去),t2=4-$\sqrt{2}$.
故当t=4-$\sqrt{2}$时,四边形PFP′C是菱形.
点评 本题考查了二次函数的性质、待定系数法求函数解析式以及三角形的面积公式,解题的关键:(1)待定系数法求函数解析式;(2)找出直线BC的解析式利用面积法求出三角形的高;(3)①结合直线BC与抛物线的解析式设出P、F点的坐标;②由菱形的判定定理找出PC=PF.本题属于中档题,(1)难度不大;(2)利用面积相等巧妙的算出三角形的高;(3)由二次函数的性质找出最值.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案| A. | m≥1 | B. | m≤1 | C. | m≥1且m≠0 | D. | m≤1且m≠0 |
| A. | 12 | B. | 14 | C. | 16 | D. | 17 |
| A. | 0 | B. | 1 | C. | -1 | D. | ±1 |
| A. | ${(\frac{1}{3})^{-2}}=-9$ | B. | (a-b)(-a-b)=a2-b2 | C. | 2a2•a3=2a6 | D. | (-a)10÷(-a)4=a6 |
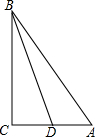 在Rt△ACB中,∠C=90°,点D是AC的中点,cos∠CBD=$\frac{{\sqrt{15}}}{4}$,则sin∠ABD=$\frac{\sqrt{285}}{76}$.
在Rt△ACB中,∠C=90°,点D是AC的中点,cos∠CBD=$\frac{{\sqrt{15}}}{4}$,则sin∠ABD=$\frac{\sqrt{285}}{76}$.