题目内容
2.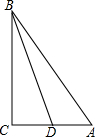 在Rt△ACB中,∠C=90°,点D是AC的中点,cos∠CBD=$\frac{{\sqrt{15}}}{4}$,则sin∠ABD=$\frac{\sqrt{285}}{76}$.
在Rt△ACB中,∠C=90°,点D是AC的中点,cos∠CBD=$\frac{{\sqrt{15}}}{4}$,则sin∠ABD=$\frac{\sqrt{285}}{76}$.
分析 过点D作DH⊥AB,如图所示.设BD=4x,可根据三角函数和勾股定理求出BC、CD(AD)、AC、AB的值(用x表示),要求sin∠ABD,只需求出DH的值(用x表示),只需证明△AHD∽△ACB,并利用相似三角形的性质就可解决问题.
解答 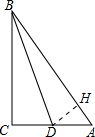 解:过点D作DH⊥AB,如图所示.
解:过点D作DH⊥AB,如图所示.
在Rt△BCD中,
cos∠CBD=$\frac{BC}{BD}$=$\frac{{\sqrt{15}}}{4}$.
设BD=4x,则BC=$\sqrt{15}$x,
∴CD=$\sqrt{(4x)^{2}-(\sqrt{15}x)^{2}}$=x.
∵点D是AC的中点,
∴AD=CD=x,
∴AC=2x,AB=$\sqrt{(\sqrt{15}x)^{2}+(2x)^{2}}$=$\sqrt{19}$x.
∵∠A=∠A,∠DHA=∠C=90°,
∴△AHD∽△ACB,
∴$\frac{DH}{BC}$=$\frac{AD}{AB}$,
∴$\frac{DH}{\sqrt{15}x}$=$\frac{x}{\sqrt{19}x}$,
∴DH=$\frac{\sqrt{285}}{19}$.
在Rt△BHD中,
sin∠ABD=$\frac{DH}{BD}$=$\frac{\sqrt{285}}{76}$.
故答案为$\frac{\sqrt{285}}{76}$.
点评 本题主要考查了三角函数的定义、相似三角形的判定与性质、勾股定理等知识,题目中若涉及到三角函数,通常需放到直角三角形中考虑.

练习册系列答案
相关题目
12.下列说法正确的是( )
| A. | 平分弦的直径垂直于弦 | B. | 相等的圆周角所对的弧相等 | ||
| C. | 三个点确定一个圆 | D. | 半圆或直径所对的圆周角是直角 |
 根据图中所表示的已知角的度数,可以求出∠α=50°.
根据图中所表示的已知角的度数,可以求出∠α=50°.
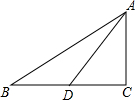 如图,在Rt△ABC中,∠ACB=90°,AD是边BC边上的中线,如果AD=BC,那么cot∠CAB的值是$\frac{\sqrt{3}}{2}$.
如图,在Rt△ABC中,∠ACB=90°,AD是边BC边上的中线,如果AD=BC,那么cot∠CAB的值是$\frac{\sqrt{3}}{2}$.