题目内容
1. 如图,已知∠C=∠D,AC=BD,AD交BC于点O,求证:AD=BC.
如图,已知∠C=∠D,AC=BD,AD交BC于点O,求证:AD=BC.
分析 由△AOC≌△BOD,推出OA=OB,OC=OD,推出OA+OD=PB+OC即AD=BC.
解答 证明:在△AOC和△BOD中,
$\left\{\begin{array}{l}{∠AOC=∠BOD}\\{∠C=∠D}\\{AC=BD}\end{array}\right.$,
∴△AOC≌△BOD,
∴OA=OB,OC=OD,
∴OA+OD=PB+OC即AD=BC,
∴AD=BC.
点评 本题考查全等三角形的判定和性质,线段的和差定义等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
9. 如图所示的图形是按下列步骤做得的:①在直线l上截取线段AB,使AB=2;②分别以A,B为圆心,以1.5为半径作弧,两弧分别交于C,D两点,连接AC,AD,BC,BD,则四边形ACBD的面积是( )
如图所示的图形是按下列步骤做得的:①在直线l上截取线段AB,使AB=2;②分别以A,B为圆心,以1.5为半径作弧,两弧分别交于C,D两点,连接AC,AD,BC,BD,则四边形ACBD的面积是( )
 如图所示的图形是按下列步骤做得的:①在直线l上截取线段AB,使AB=2;②分别以A,B为圆心,以1.5为半径作弧,两弧分别交于C,D两点,连接AC,AD,BC,BD,则四边形ACBD的面积是( )
如图所示的图形是按下列步骤做得的:①在直线l上截取线段AB,使AB=2;②分别以A,B为圆心,以1.5为半径作弧,两弧分别交于C,D两点,连接AC,AD,BC,BD,则四边形ACBD的面积是( )| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
13.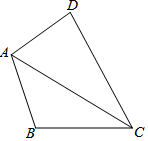 如图,四边形ABCD中,AB=AD,∠B+∠D=180°,若AC=12,则四边形ABCD的面积最大值为( )
如图,四边形ABCD中,AB=AD,∠B+∠D=180°,若AC=12,则四边形ABCD的面积最大值为( )
 如图,四边形ABCD中,AB=AD,∠B+∠D=180°,若AC=12,则四边形ABCD的面积最大值为( )
如图,四边形ABCD中,AB=AD,∠B+∠D=180°,若AC=12,则四边形ABCD的面积最大值为( )| A. | 36 | B. | $36\sqrt{2}$ | C. | 72 | D. | $72\sqrt{2}$ |
10.若代数式-3a-x+1by-2与2a2x-2b是同类项,则x-y的值为( )
| A. | -2 | B. | 2 | C. | -3 | D. | 3 |
 如图,∠BAD=90°,射线AC平分∠BAE.
如图,∠BAD=90°,射线AC平分∠BAE.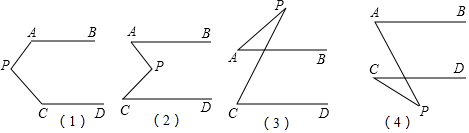
 如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P.则tan∠APD的值是( )
如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P.则tan∠APD的值是( )