题目内容
9.如图,已知AB∥CD,分别探究下面四个图形中∠APC和∠PAB,∠PCD的关系,请你从所得四个关系中任意选出一个,说明你探究结论的正确性.结论:(1)∠APC=360°-∠PAB-∠PCD;(2)∠APC=∠PAB+∠PCD;(3)∠APC=∠PCD-∠PAB;(4)∠APC=∠PAB-∠PCD.
选择结论(2),说明理由.
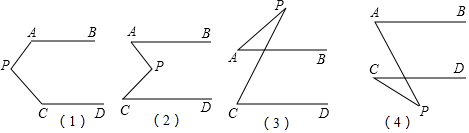
分析 (1)过点P作PE∥AB,则PE∥CD,根据平行线的性质可得∠APE+∠PAB=180°、∠CPE+∠PCD=180°,再根据∠APC=∠APE+∠CPE即可得出∠APC=360°-∠PAB-∠PCD;
(2)过点P作PF∥AB,则PF∥CD,根据平行线的性质可得∠APF=∠PAB、∠CPF=∠PCD,再根据∠APC=∠APF+∠CPF即可得出∠APC=∠PAB+∠PCD;
(3)过点P作PM∥AB,则PM∥CD,根据平行线的性质可得∠APM=180°-∠PAB、∠CPM=180°-∠PCD,再根据∠APC=∠APM-∠CPM即可得出∠APC=∠PCD-∠PAB;
(4)过点P作PN∥AB,则PN∥CD,根据平行线的性质可得∠APN=180°-∠PAB、∠CPN=180°-∠PCD,再根据∠APC=∠CPN-∠APN即可得出∠APC=∠PAB-∠PCD.
解答 解:(1)∠APC=360°-∠PAB-∠PCD,理由如下:
过点P作PE∥AB,
∵AB∥CD,PE∥AB,
∴PE∥CD,
∴∠APE+∠PAB=180°,∠CPE+∠PCD=180°.
∵∠APC=∠APE+∠CPE,
∴∠APC=180°-∠PAB+180°-∠PCD=360°-∠PAB-∠PCD.
(2)∠APC=∠PAB+∠PCD,理由如下:
过点P作PF∥AB,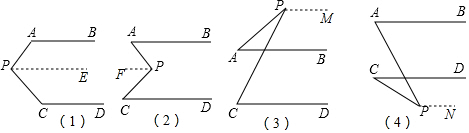
∵AB∥CD,PF∥AB,
∴PF∥CD,
∴∠APF=∠PAB,∠CPF=∠PCD.
∵∠APC=∠APF+∠CPF,
∴∠APC=∠PAB+∠PCD.
(3)∠APC=∠PCD-∠PAB,理由如下:
过点P作PM∥AB,则PM∥CD,
∴∠APM=180°-∠PAB,∠CPM=180°-∠PCD,
∴∠APC=∠APM-∠CPM=(180°-∠PAB)-(180°-∠PCD)=∠PCD-∠PAB.
(4)∠APC=∠PAB-∠PCD,理由如下:
过点P作PN∥AB,则PN∥CD,
∴∠APN=180°-∠PAB,∠CPN=180°-∠PCD,
∴∠APC=∠CPN-∠APN=(180°-∠PCD)-(180°-∠PAB)=∠PAB-∠PCD..
故答案为:(1)∠APC=360°-∠PAB-∠PCD;(2)∠APC=∠PAB+∠PCD;(3)∠APC=∠PCD-∠PAB;(4)∠APC=∠PAB-∠PCD.
点评 本题考查了平行线的性质,解题的关键是:(1)根据平行线的性质找出∠APE+∠PAB=180°、∠CPE+∠PCD=180°;(2)根据平行线的性质找出∠APF=∠PAB、∠CPF=∠PCD;(3)根据平行线的性质找出∠APM=180°-∠PAB、∠CPM=180°-∠PCD;(4)根据平行线的性质找出∠APN=180°-∠PAB、∠CPN=180°-∠PCD.

| A. | 只有① | B. | 只有② | C. | ①和② | D. | ①和③ |
 如图,在△ABC中,点D、E、F分别是AB、AC、BC的中点,现以线段AC,BC为斜边向△ABC的外侧作直角三角形,分别是△APC、△BQC,且DP=DQ
如图,在△ABC中,点D、E、F分别是AB、AC、BC的中点,现以线段AC,BC为斜边向△ABC的外侧作直角三角形,分别是△APC、△BQC,且DP=DQ 如图中,正方形ABCD的面积是64m2,DC与EC的长度比是5:3,求三角形CDE的面积.(用比例解)
如图中,正方形ABCD的面积是64m2,DC与EC的长度比是5:3,求三角形CDE的面积.(用比例解)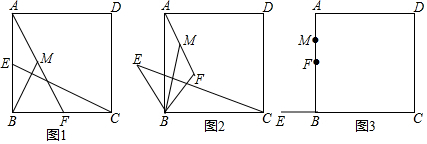
 如图,已知∠C=∠D,AC=BD,AD交BC于点O,求证:AD=BC.
如图,已知∠C=∠D,AC=BD,AD交BC于点O,求证:AD=BC.