题目内容
13.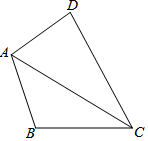 如图,四边形ABCD中,AB=AD,∠B+∠D=180°,若AC=12,则四边形ABCD的面积最大值为( )
如图,四边形ABCD中,AB=AD,∠B+∠D=180°,若AC=12,则四边形ABCD的面积最大值为( )| A. | 36 | B. | $36\sqrt{2}$ | C. | 72 | D. | $72\sqrt{2}$ |
分析 解:过A点分别作AE⊥BC于E,AF⊥CD于F,连接EF,根据全等三角形的性质得到AE=AF,S四边形ABCD=S四边形AECF,当四边形AECF的面积最大时,四边形AECF是正方形,根据正方形的性质得到EF=AC,EF⊥AC,于是得到结论.
解答 解: 过A点分别作AE⊥BC于E,AF⊥CD于F,连接EF,
过A点分别作AE⊥BC于E,AF⊥CD于F,连接EF,
∵∠ADF+∠ABC=180°,且∠ABE+∠ABC=180°,
∴∠ADF=∠ABE,在△ABE与△ADF中,$\left\{\begin{array}{l}{∠E=∠AFD}\\{∠ABE=∠ADC}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△ADF,
∴AE=AF,S四边形ABCD=S四边形AECF=$\frac{1}{2}$•AC•EF
当EF=AC时,四边形AECF的面积最大,此时四边形AECF是正方形,
∴EF=AC,EF⊥AC,
∴四边形ABCD的面积最大值=$\frac{1}{2}$AC2=$\frac{1}{2}$×122=72,
故选C.
点评 本题考查了全等三角形的判断和性质,角平分线的性质,正方形的面积的计算,正确的作出辅助线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5. 有理数a,b在数轴上的位置如图所示,则|a+b|+|a-b|化简的结果为( )
有理数a,b在数轴上的位置如图所示,则|a+b|+|a-b|化简的结果为( )
 有理数a,b在数轴上的位置如图所示,则|a+b|+|a-b|化简的结果为( )
有理数a,b在数轴上的位置如图所示,则|a+b|+|a-b|化简的结果为( )| A. | -2b | B. | -2a | C. | 2b | D. | 0 |
2.在下列式子:①$\frac{1}{x-2}$②(x-2)0③$\sqrt{x-2}$中,x不可以取到2的是( )
| A. | 只有① | B. | 只有② | C. | ①和② | D. | ①和③ |
 如图中,正方形ABCD的面积是64m2,DC与EC的长度比是5:3,求三角形CDE的面积.(用比例解)
如图中,正方形ABCD的面积是64m2,DC与EC的长度比是5:3,求三角形CDE的面积.(用比例解) 如图,已知∠C=∠D,AC=BD,AD交BC于点O,求证:AD=BC.
如图,已知∠C=∠D,AC=BD,AD交BC于点O,求证:AD=BC.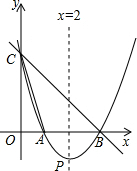 如图,直线y=-x+3与x轴、y轴分别相交于点B、C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一个交点为A,顶点为P,且对称轴为直线x=2.
如图,直线y=-x+3与x轴、y轴分别相交于点B、C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一个交点为A,顶点为P,且对称轴为直线x=2.