题目内容
15.已知有理数a、b满足|a+3b+4|+|b+2|=b+2,且|2a+b|=7,则ab=$\frac{17}{25}$.分析 首先根据绝对值的非负性得出b+2≥0,那么|b+2|=b+2,进而得到a+3b+4=0①,2a+b=-7②,①与②联立,求出a=-$\frac{17}{5}$,b=-$\frac{1}{5}$,代入ab计算即可.
解答 解:∵|a+3b+4|+|b+2|=b+2,
∴b+2≥0,
∴|b+2|=b+2,
∴|a+3b+4|=0,
∴a+3b+4=0①,
∵|2a+b|=7,
∴2a+b=-7②,
①与②联立,解得a=-$\frac{17}{5}$,b=-$\frac{1}{5}$,
∴ab=(-$\frac{17}{5}$)×(-$\frac{1}{5}$)=$\frac{17}{25}$.
故答案为$\frac{17}{25}$.
点评 本题考查了整式的加减,二元一次方程组的解法,绝对值,代数式求值,正确求出a与b的值是解题的关键.

练习册系列答案
相关题目
3.若x<0,则|$\sqrt{{x}^{2}}$+3x|=( )
| A. | -4x | B. | 4x | C. | -2x | D. | 2x |
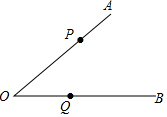 已知点P、Q分别在∠ACB的边OA、OB上,按下列要求画图
已知点P、Q分别在∠ACB的边OA、OB上,按下列要求画图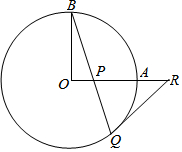 如图,OA和OB是⊙O的半径,并且OA⊥OB.P是OA上任意一点,BP的延长线交⊙O于点Q,点R在OA的延长线上,且RP=RQ.
如图,OA和OB是⊙O的半径,并且OA⊥OB.P是OA上任意一点,BP的延长线交⊙O于点Q,点R在OA的延长线上,且RP=RQ.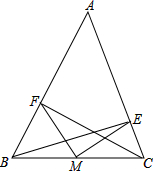 如图所示,BE,CF是△ABC的两条高,M为BC中点,连接MF,ME.
如图所示,BE,CF是△ABC的两条高,M为BC中点,连接MF,ME.