题目内容
7.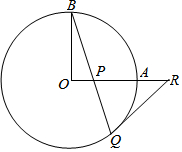 如图,OA和OB是⊙O的半径,并且OA⊥OB.P是OA上任意一点,BP的延长线交⊙O于点Q,点R在OA的延长线上,且RP=RQ.
如图,OA和OB是⊙O的半径,并且OA⊥OB.P是OA上任意一点,BP的延长线交⊙O于点Q,点R在OA的延长线上,且RP=RQ.(1)求证:RQ是⊙O的切线;
(2)当RA≤OA时,试确定∠B的取值范围;
(3)求证:OB2=PB•PQ+OP2.
分析 (1)连接OQ.欲证明RQ是⊙O的切线,只要证明∠OQR=90°.
(2)求出两个特殊位置的∠B的值即可解决问题.
(3)如图2中,延长AO交⊙于M.由PA•PM=PB•PQ(相交弦定理,也可以连接BM、AQ证明△PBM∽△PAQ得到),推出(OB-OP)(OB+OP)=PB•PQ,可得OB2-OP2=PB•PQ.
解答 (1)证明:连接OQ.
∵OA⊥OB,
∴∠2+∠B=90°,
∵OB=OQ,
∴∠B=∠4,
∵RP=RQ,
∴∠1=∠3=∠2,
∴∠3+∠4=90°,
∴OQ⊥RQ,
∴RQ是⊙O的切线.
(2)解:如图1中,
①当点R与A重合时,易知∠B=45°.
②当AR=OA时,在Rt△ORQ中,∵∠OQR=90°,OR=2OQ,
∴∠R=30°,
∵RQ=RP,
∴∠RPQ=∠RQP=75°,
∴∠OPB=75°,
∴∠B=90°-∠OPB=15°,
综上所述,15°≤∠B<45°.
(3)如图2中,延长AO交⊙于M.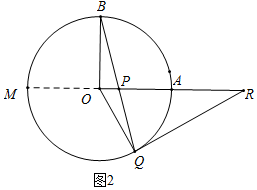
∵PA•PM=PB•PQ(相交弦定理,也可以连接BM、AQ证明△PBM∽△PAQ得到),
∴(OB-OP)(OB+OP)=PB•PQ,
∴OB2-OP2=PB•PQ.
即OB2=PB•PQ+OP2.
点评 本题考查圆综合题、切线的判定和性质、等腰三角形的性质、相交弦定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考压轴题.

练习册系列答案
相关题目
12. 用40cm长的绳子围成矩形ABCD,设AB=xm,矩形ABCD的面积为S(m2)
用40cm长的绳子围成矩形ABCD,设AB=xm,矩形ABCD的面积为S(m2)
(1)求S关于x的函数解析式及x的取值范围
(2)写出下面表格中与x相对应的S的值
(3)猜一猜,当x为何值时,S的值最大?
 用40cm长的绳子围成矩形ABCD,设AB=xm,矩形ABCD的面积为S(m2)
用40cm长的绳子围成矩形ABCD,设AB=xm,矩形ABCD的面积为S(m2)(1)求S关于x的函数解析式及x的取值范围
(2)写出下面表格中与x相对应的S的值
| x | … | 8 | 9 | 9.5 | 10 | 10.5 | 11 | 12 | … |
| S | … | 96 | 99 | 99.75 | 100 | 99,75 | 99 | 96 | … |
19.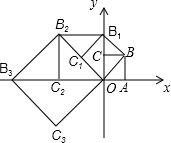 如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2015的坐标为( )
如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2015的坐标为( )
 如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2015的坐标为( )
如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2015的坐标为( )| A. | (21008,0) | B. | (21007,-21007) | C. | (21009,21009) | D. | (-21007,21007) |

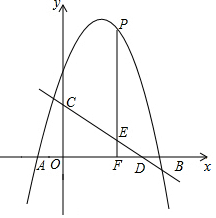 如图,抛物线y=-x2+4x+5与x轴交于A,B两点(点A在点B的左侧),直线y=$-\frac{3}{4}x+3$与y轴交于点C,与x轴交于点D.P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.
如图,抛物线y=-x2+4x+5与x轴交于A,B两点(点A在点B的左侧),直线y=$-\frac{3}{4}x+3$与y轴交于点C,与x轴交于点D.P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.