题目内容
4．
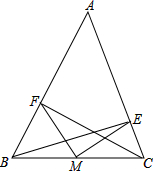如图所示，BE，CF是△ABC的两条高，M为BC中点，连接MF，ME．求证：ME=MF．
分析 根据直角三角形斜边上的中线等于斜边的一半，可得ME=$\frac{1}{2}$BC，MF=$\frac{1}{2}$BC，从而得出ME=MF．
解答 证明：∵BE是△ABC的高，M为BC的中点，
∴ME=$\frac{1}{2}$BC，
∵CF是△ABC的高，M为BC的中点，
∴MF=$\frac{1}{2}$BC，
∴ME=MF．
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质，熟记性质是解题的关键．
练习册系列答案
相关题目
12．
用40cm长的绳子围成矩形ABCD，设AB=xm，矩形ABCD的面积为S（m2）
（1）求S关于x的函数解析式及x的取值范围
（2）写出下面表格中与x相对应的S的值
（3）猜一猜，当x为何值时，S的值最大？
用40cm长的绳子围成矩形ABCD，设AB=xm，矩形ABCD的面积为S（m2）（1）求S关于x的函数解析式及x的取值范围
（2）写出下面表格中与x相对应的S的值
| x | … | 8 | 9 | 9.5 | 10 | 10.5 | 11 | 12 | … |
| S | … | 96 | 99 | 99.75 | 100 | 99，75 | 99 | 96 | … |
19．
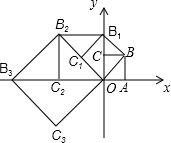如图，在平面直角坐标系中有一边长为1的正方形OABC，边OA、OC分别在x轴、y轴上，如果以对角线OB为边作第二个正方形OBB1C1，再以对角线OB1为边作第三个正方形OB1B2C2，照此规律作下去，则点B2015的坐标为（ ）
如图，在平面直角坐标系中有一边长为1的正方形OABC，边OA、OC分别在x轴、y轴上，如果以对角线OB为边作第二个正方形OBB1C1，再以对角线OB1为边作第三个正方形OB1B2C2，照此规律作下去，则点B2015的坐标为（ ）| A． | （21008，0） | B． | （21007，-21007） | C． | （21009，21009） | D． | （-21007，21007） |
13．如图在一个边长为a的小正方形中，剪去一个边长为b的小正方形，再将余下的部分拼成一个长方形．
（1）两个图形（着色部分）的面积之间有什么关系？
（2）请结合图形，对平方差公式（a+b）（a-b）=a2-b2进行解释．
（1）两个图形（着色部分）的面积之间有什么关系？
（2）请结合图形，对平方差公式（a+b）（a-b）=a2-b2进行解释．
| 算式 | 与平方差公式a对应的项 | 与平方差公式中b对应的项 | 写成a2-b2的形式 | 计算结果 |
| （x+y）（x-y） | x | y | x2-y2 | x2-y2 |
| （m+3）（m-3） | m | 3 | m2-32 | m2-9 |
| （2x+1）（2x-1） | 2x | 1 | （2m）2-12 | 4m2-1 |
| （x+2y）（-x+2y） | x | 2y | x2-（2y）2 | x2-4y2 |