Question

20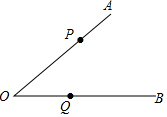．已知点P、Q分别在∠ACB的边OA、OB上，按下列要求画图
（1）画直线PQ；
（2）过点Q画射线OA的垂直线段DQ，垂足为点D；
（3）若DQ平分∠PQO，∠POQ=54°，求∠PQB的度数．

Answer 1

分析 （1）过点O、点Q作直线即可；
（2）过点Q作QD⊥AO于D即可；
（3）根据∠POQ=54°，QD⊥AO，即可得出∠OQD=36°，再根据DQ平分∠PQO，即可得到∠PQO=72°，进而得出∠PQB=180°-∠PQO=108°．

解答 解：（1）如图所示，直线PQ即为所求；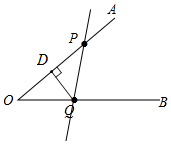

（2）如图所示，线段DQ即为所求；
（3）∵∠POQ=54°，QD⊥AO，
∴∠OQD=36°，
又∵DQ平分∠PQO，
∴∠PQO=2∠OQD=72°，
∴∠PQB=180°-∠PQO=108°．

点评 本题主要考查了基本作图以及角平分线的定义的运用，解决问题的关键是根据直角三角形的两个锐角互余以及邻补角的定义进行计算求解．