题目内容
10.已知点(-1,a)和点($\frac{1}{2}$,b)都在直线y=$\frac{2}{3}$x+3上,试比较a和b的大小,你能想出几种判断方法?分析 (方法一)由k>0结合一次函数的性质即可得出y随x的增大而增大,再根据-1和$\frac{1}{2}$的大小即可得出a和b的大小;
(方法二)根据一次函数图象上点的坐标特征求出a、b的值,比较后即可得出结论.
解答 解:(方法一)∵在直线y=$\frac{2}{3}$x+3中k=$\frac{2}{3}$>0,
∴直线y=$\frac{2}{3}$x+3中y随x的增大而增大.
∵-1<$\frac{1}{2}$,
∴a<b.
(方法二)∵点(-1,a)和点($\frac{1}{2}$,b)都在直线y=$\frac{2}{3}$x+3上,
∴a=$\frac{2}{3}$×(-1)+3=$\frac{1}{3}$,b=$\frac{2}{3}$×$\frac{1}{2}$+3=$\frac{10}{3}$.
∵$\frac{1}{3}$<$\frac{10}{3}$,
∴a<b.
点评 本题考查了一次函数图象上点的坐标特征以及一次函数的性质,根据一次函数的性质找出函数的单调性(或根据一次函数图象上点的坐标特征求出a、b的值).

练习册系列答案
相关题目
19.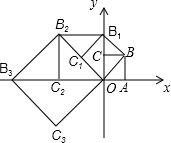 如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2015的坐标为( )
如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2015的坐标为( )
 如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2015的坐标为( )
如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2015的坐标为( )| A. | (21008,0) | B. | (21007,-21007) | C. | (21009,21009) | D. | (-21007,21007) |
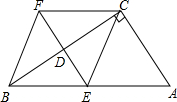 如图所示,在四边形ABFC,∠ACB=90°,BC垂直平分线EF交BC于点D,交AB于点E,且CF=AE
如图所示,在四边形ABFC,∠ACB=90°,BC垂直平分线EF交BC于点D,交AB于点E,且CF=AE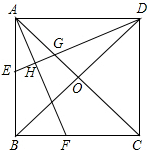 已知,如图,在正方形ABCD中,O是对角线的交点,AF平分∠BAC,DH⊥AF于点H,交AC于点G,DH延长线交AB于点E.
已知,如图,在正方形ABCD中,O是对角线的交点,AF平分∠BAC,DH⊥AF于点H,交AC于点G,DH延长线交AB于点E. 如图,在直角坐标系中,点A是反比例函数y1=$\frac{k}{x}$图象上一点,AB⊥x轴的正半轴于点B,点C是OB的中点,一次函数y2=ax+b的图象经过A、C两点,交y轴于点D(0,-2),△AOB的面积为4
如图,在直角坐标系中,点A是反比例函数y1=$\frac{k}{x}$图象上一点,AB⊥x轴的正半轴于点B,点C是OB的中点,一次函数y2=ax+b的图象经过A、C两点,交y轴于点D(0,-2),△AOB的面积为4