题目内容
2.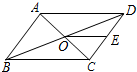 如图,?ABCD的周长为28,对角线AC、BD相交于点O.点E是CD的中点,BD=10,则△DOE的周长为( )
如图,?ABCD的周长为28,对角线AC、BD相交于点O.点E是CD的中点,BD=10,则△DOE的周长为( )| A. | 28 | B. | 24 | C. | 12 | D. | 17 |
分析 由平行四边形的性质和已知条件得出OD=5,CD+BC=14,再证明OE是△BCD的中位线,得出DE+OE=7,即可得出结果.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OB=OD=$\frac{1}{2}$BD=5,
∵?ABCD的周长为28,
∴CD+BC=14,
∵点E是CD的中点,
∴DE=$\frac{1}{2}$CD,OE是△BCD的中位线,
∴OE=$\frac{1}{2}$BC,
∴DE+OE=$\frac{1}{2}$(CD+BC)=7,
∴△DOE的周长=OD+DE+OE=5+7=12;
故选:C.
点评 本题考查了平行四边形的性质、三角形中位线定理;熟练掌握平行四边形的性质,运用三角形中位线定理是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在△ABC上,点D、E分别是AC、BC边上的点,AE与BD交于点O,且CD=CE,∠1=∠2.
如图,在△ABC上,点D、E分别是AC、BC边上的点,AE与BD交于点O,且CD=CE,∠1=∠2.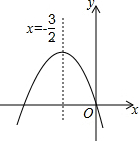 如图,已知二次函数y=ax2+bx+c的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④4ac-b2<0.其中正确结论有①③④.
如图,已知二次函数y=ax2+bx+c的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④4ac-b2<0.其中正确结论有①③④. 某企业接到一批茶杯生产任务,按要求在15天内完成,预定这批茶杯的出厂价为每个6元,为按时完成任务,该企业招收了新工人,设新工人小王第x天生产的茶杯数量为y个,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$.
某企业接到一批茶杯生产任务,按要求在15天内完成,预定这批茶杯的出厂价为每个6元,为按时完成任务,该企业招收了新工人,设新工人小王第x天生产的茶杯数量为y个,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$.
 如图,长方形的长与宽分别为a,b,它的周长为16,面积为10.求a2b+ab2的值.
如图,长方形的长与宽分别为a,b,它的周长为16,面积为10.求a2b+ab2的值.