题目内容
11.若一个多边形的每个内角都为135°,则它的边数为8.分析 由一个正多边形的每个内角都为135°,可求得其外角的度数,继而可求得此多边形的边数,则可求得答案.
解答 :∵一个正多边形的每个内角都为135°,
∴这个正多边形的每个外角都为:180°-135°=45°,
∴这个多边形的边数为:360°÷45°=8,
故答案为:8.
点评 此题考查了多边形的内角和与外角和的知识.此题难度不大,注意掌握多边形的内角和与外角和定理是关键.

练习册系列答案
相关题目
2.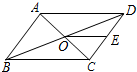 如图,?ABCD的周长为28,对角线AC、BD相交于点O.点E是CD的中点,BD=10,则△DOE的周长为( )
如图,?ABCD的周长为28,对角线AC、BD相交于点O.点E是CD的中点,BD=10,则△DOE的周长为( )
 如图,?ABCD的周长为28,对角线AC、BD相交于点O.点E是CD的中点,BD=10,则△DOE的周长为( )
如图,?ABCD的周长为28,对角线AC、BD相交于点O.点E是CD的中点,BD=10,则△DOE的周长为( )| A. | 28 | B. | 24 | C. | 12 | D. | 17 |
19.下列计算正确的是( )
| A. | a3+a3=a6 | B. | (2a)3=2a3 | C. | (a3)2=a5 | D. | a•a5=a6 |
6.(-2a)2的计算结果是( )
| A. | -4a2 | B. | 2a2 | C. | 4a | D. | 4a2 |
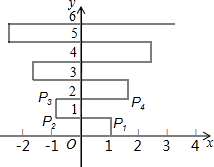 如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,P4的坐标是(2,2),点P第8次跳动至P8的坐标为(3,4);则点P第256次跳动至P256的坐标是(65,128).
如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,P4的坐标是(2,2),点P第8次跳动至P8的坐标为(3,4);则点P第256次跳动至P256的坐标是(65,128).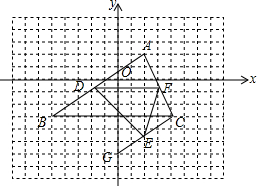 【阅读理解】
【阅读理解】