题目内容
10. 某企业接到一批茶杯生产任务,按要求在15天内完成,预定这批茶杯的出厂价为每个6元,为按时完成任务,该企业招收了新工人,设新工人小王第x天生产的茶杯数量为y个,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$.
某企业接到一批茶杯生产任务,按要求在15天内完成,预定这批茶杯的出厂价为每个6元,为按时完成任务,该企业招收了新工人,设新工人小王第x天生产的茶杯数量为y个,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$.(1)小王第几天生产的茶杯数量为420个?
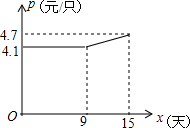
(2)如图,设第x天每个茶杯成本为P元,P与x之间的关系可用图中的函数图象来表示,若小王第x天创造的利润为W元,求W关于x的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)
分析 (1)根据y=420,求出自变量x的值即可.
(2)分三个区间求W:①当0<x≤5,②当5<x≤9.③当9<x≤15,分别根据利润=出厂价-成本计算即可.然后利用函数的性质确定最大值.
解答 解:(1)由题意30x+120=420,解得x=10,所以小王第10天生产的茶杯数量为420个.
(2)当0<x≤5时,W=6×54x-4.1×54x=102.6x,
当5<x≤9时,W=6(30x+120)-4.1(30x+120)=57x+158.
当9<x≤15时,设P=kx+b,由题意得$\left\{\begin{array}{l}{9k+b=4.1}\\{15k+b=4.7}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=0.1}\\{b=3.2}\end{array}\right.$,则p=0.1x+3.2,
则W=(30x+120)(6-0.1x-3.2)=-3x2+72x+336.
综上所述W=$\left\{\begin{array}{l}{102.6x}&{(0<x≤5)}\\{57x+158}&{(5<x≤9)}\\{-3{x}^{2}+72x+336}&{(9<x≤15)}\end{array}\right.$,
∵x=5时,W=513,
x=9时,W=671,
W=-3x2+72x+336=-3(x-12)2+768,
∴x=12时,W最大值=768.
∴第12天利润最大,最大利润为768元.
点评 本题考查一次函数的应用、二次函数的应用,解题的关键是理解题意,记住利润=出厂价-成本,学会利用函数的性质解决最值问题,属于中考常考题型.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
2.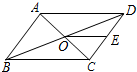 如图,?ABCD的周长为28,对角线AC、BD相交于点O.点E是CD的中点,BD=10,则△DOE的周长为( )
如图,?ABCD的周长为28,对角线AC、BD相交于点O.点E是CD的中点,BD=10,则△DOE的周长为( )
 如图,?ABCD的周长为28,对角线AC、BD相交于点O.点E是CD的中点,BD=10,则△DOE的周长为( )
如图,?ABCD的周长为28,对角线AC、BD相交于点O.点E是CD的中点,BD=10,则△DOE的周长为( )| A. | 28 | B. | 24 | C. | 12 | D. | 17 |
19.下列计算正确的是( )
| A. | a3+a3=a6 | B. | (2a)3=2a3 | C. | (a3)2=a5 | D. | a•a5=a6 |
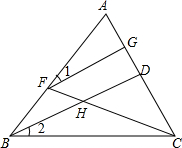 如图,已知BD平分∠ABC,点F在AB上,点G在AC上,连接FG、FC,FC与BD相交于点H,如果∠GFH与∠BHC互补.求证:∠1=∠2.
如图,已知BD平分∠ABC,点F在AB上,点G在AC上,连接FG、FC,FC与BD相交于点H,如果∠GFH与∠BHC互补.求证:∠1=∠2.
 【阅读理解】
【阅读理解】